《2025年家庭作业八年级数学上册北师大版》

【例1】在同一平面直角坐标系中，画出函数 $ y = -4x $，$ y = -1.5x $ 的图象。并根据图象回答，随着 $ x $ 值的增大，哪个函数值减小得更快？
[听课笔记]
__________________
名师点拨 画正比例函数 $ y = kx $ 的图象，一般选择过点 $ (0,0) $ 和 $ (1,k) $ 画直线。当自变量的系数是分数时，点的选择要灵活，如画函数 $ y = -\frac{3}{2}x $ 的图象，可以选择过点 $ (0,0) $ 和 $ (-2,3) $ 画直线。

答案：
解如图， 从图象可以看出，随着$x$值的增大，$y = -4x$的函数值减小得更快。

【对点训练1】在同一直角坐标系中，画出函数 $ y = \frac{1}{5}x $，$ y = x $，$ y = 5x $ 的图象，然后比较哪一个与 $ x $ 轴正方向所成的锐角最小，由此你有什么猜想？再画几个图象验证你的猜想。

答案：
解如图， 由以上三个函数的图象可知函数$y = \frac{1}{5}x$与$x$轴正方向所成的锐角最小，由此可知在正比例函数$y = kx(k ＞ 0)$中，$k$越小，函数图象与$x$轴正方向所成的锐角越小。再画出函数$y = \frac{1}{2}x$与函数$y = 2x$的图象进行比较。

【例2】根据表中正比例函数的自变量 $ x $ 与函数 $ y $ 的对应值，求出正比例函数的表达式。

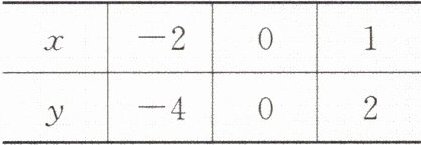
[听课笔记]
__________________
名师点拨 正比例函数只含有一个待定系数，因此，只需要知道一个点（除原点外）的坐标即可求正比例函数的表达式。

答案： 解设正比例函数的表达式为$y = kx(k \neq 0)$，当$x = -2$时，$y = -4$，则$-4 = -2k$，解得$k = 2$，故正比例函数的表达式为$y = 2x$。

【对点训练2】已知点 $ (2,-3) $ 在正比例函数 $ y = kx(k \neq 0) $ 的图象上，则 $ y $ 的值随 $ x $ 值的增大而减小(填“增大”或“减小”)。

答案： 减小