第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
【对点训练】某工厂加工一批产品,为了提前交货,规定每个工人完成$100$个及以内(含$100$个),每个产品付酬$1.5$元;超过$100$个,但不超过$200$个的部分每个产品付酬增加$0.3$元;超过$200$个的部分,每个产品再增加$0.4$元。求一个工人:
(1)完成$100$个及以内(含$100$个)所得报酬$y$(单位:元)与产品数$x$(单位:个)之间的关系式;
(2)完成$100$个以上,但不超过$200$个所得报酬$y$(单位:元)与产品数$x$(单位:个)之间的关系式;
(3)完成$200$个以上所得报酬$y$(单位:元)与产品数$x$(单位:个)之间的关系式。
(1)完成$100$个及以内(含$100$个)所得报酬$y$(单位:元)与产品数$x$(单位:个)之间的关系式;
(2)完成$100$个以上,但不超过$200$个所得报酬$y$(单位:元)与产品数$x$(单位:个)之间的关系式;
(3)完成$200$个以上所得报酬$y$(单位:元)与产品数$x$(单位:个)之间的关系式。
答案:
(1)当0≤x≤100时,y=1.5x。
(2)当100<x≤200时,y=1.5x+(x-100)×0.3=1.8x-30。
(3)当x>200时,y=1.5x+(x-100)×0.3+(x-200)×0.4=2.2x-110。
(1)当0≤x≤100时,y=1.5x。
(2)当100<x≤200时,y=1.5x+(x-100)×0.3=1.8x-30。
(3)当x>200时,y=1.5x+(x-100)×0.3+(x-200)×0.4=2.2x-110。
1.匀速地向如图所示的容器(容器厚度不计)内注水,直到把容器注满。在注水过程中,容器内水面高度$h$随时间$t$变化的大致图象是(
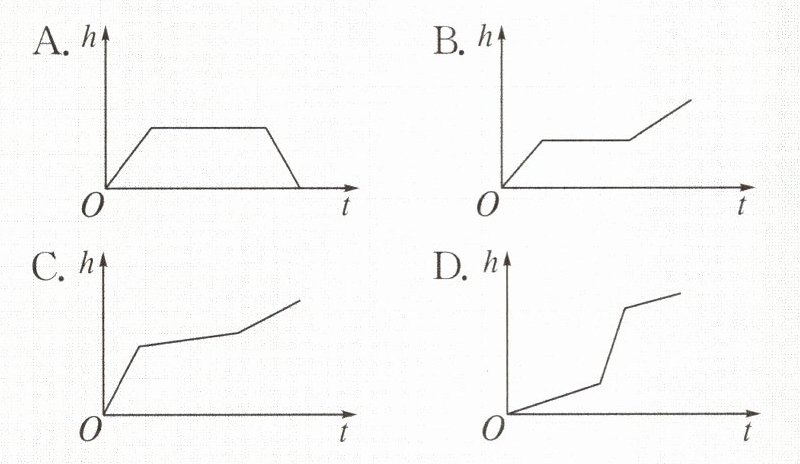

A.$h \uparrow$
B.$h \uparrow$
$O$ $t$ $O$ $t$
C.$h \uparrow$
D.$h \uparrow$
$O$ $t$ $O$ $t$
C
)。

A.$h \uparrow$
B.$h \uparrow$
$O$ $t$ $O$ $t$
C.$h \uparrow$
D.$h \uparrow$
$O$ $t$ $O$ $t$
答案:
1.C
2.为响应“低碳生活”的号召,明明决定每天骑自行车上学,有一天明明骑了$1000\ {m}$后,自行车发生了故障,修车耽误了$5\ {min}$,车修好后明明继续骑行,以相同的速度用了$8\ {min}$骑行了剩余的$800\ {m}$,到达学校(假设在骑车过程中匀速行驶)。若设他从家开始去学校的时间为$t$(单位:${min}$),离家的路程为$y$(单位:${m}$),则当$15 < t \leq 23$时,$y$与$t$之间的关系式为(
A.$y = 100t(15 < t \leq 23)$
B.$y = 100t - 500(15 < t \leq 23)$
C.$y = 50t + 650(15 < t \leq 23)$
D.$y = 100t + 500(15 < t \leq 23)$
B
)。A.$y = 100t(15 < t \leq 23)$
B.$y = 100t - 500(15 < t \leq 23)$
C.$y = 50t + 650(15 < t \leq 23)$
D.$y = 100t + 500(15 < t \leq 23)$
答案:
2.B
3.某市为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过$14\ {t}$时,每吨按政府补贴优惠价收费;每月超过$14\ {t}$时,超过部分每吨按市场调节价收费,每吨水的政府补贴优惠价为$1$元,市场调节价为$2.5$元。设每月用水量为$x\ {t}$,应交水费为$y$元,则当$x > 14$时,$y$与$x$之间的关系式是(
A.$y = x(x > 14)$
B.$y = 2.5x - 21(x > 14)$
C.$y = 2.5x + 14(x > 14)$
D.$y = 3.5x - 21(x > 14)$
B
)。A.$y = x(x > 14)$
B.$y = 2.5x - 21(x > 14)$
C.$y = 2.5x + 14(x > 14)$
D.$y = 3.5x - 21(x > 14)$
答案:
3.B
4.根据如图所示的程序计算函数$y$的值,若输入$x$的值是$2$,则输出$y$的值是$1$,若输入$x$的值是$7$,则输出$y$的值是
$\begin{aligned}&输入x \begin{cases}x\geq3 \rightarrow y=\frac{-x+b}{2} \rightarrow输出y\\x<3 \rightarrow y=-2x+b\end{cases} \end{aligned}$
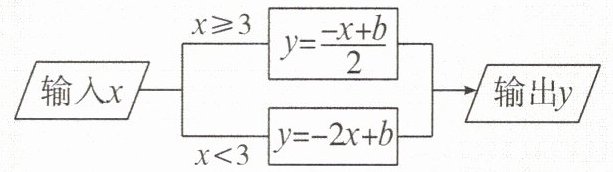
-1
。$\begin{aligned}&输入x \begin{cases}x\geq3 \rightarrow y=\frac{-x+b}{2} \rightarrow输出y\\x<3 \rightarrow y=-2x+b\end{cases} \end{aligned}$
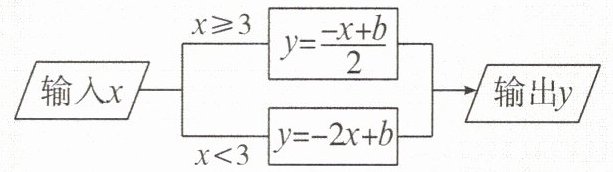
答案:
4.-1
查看更多完整答案,请扫码查看


