第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
3.$\sqrt{1843}$的值介于(
A.25与30之间
B.30与35之间
C.35与40之间
D.40与45之间
D
)。A.25与30之间
B.30与35之间
C.35与40之间
D.40与45之间
答案:
D
4.已知$a=\sqrt{5}$,$b=2$,$c=\sqrt{3}$,则$a$,$b$,$c$的大小关系是(
A.$b>a>c$
B.$a>c>b$
C.$a>b>c$
D.$b>c>a$
C
)。A.$b>a>c$
B.$a>c>b$
C.$a>b>c$
D.$b>c>a$
答案:
C
5.利用计算器求下列各式的值(结果精确到0.01):
(1)$\frac{\sqrt{5}}{2}+\sqrt[3]{2}-\pi$;(2)$\sqrt{11}×\sqrt{2}÷\frac{1}{\sqrt{6}}$。
(1)$\frac{\sqrt{5}}{2}+\sqrt[3]{2}-\pi$;(2)$\sqrt{11}×\sqrt{2}÷\frac{1}{\sqrt{6}}$。
答案:
(1)−0.76;
(2)11.49
(1)−0.76;
(2)11.49
6.读了《曹冲称象》的故事后,亮亮深受启发,他利用排水法测出了正方体物块的体积(即物块的体积等于排出的水的体积)。如图,他将一个正方体物块悬挂后完全浸入盛满水的烧杯中(绳子的体积忽略不计),水溢出至一个量筒中,测得溢出的水的体积为50 $cm^3$。由此,可估计该正方体物块的棱长位于(
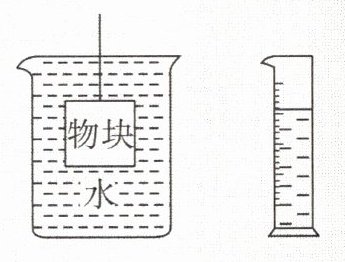
A.1和2之间
B.2和3之间
C.3和4之间
D.4和5之间
C
)。
A.1和2之间
B.2和3之间
C.3和4之间
D.4和5之间
答案:
C
7.已知$a$,$b$,$n$均为正整数。
(1)若$n<\sqrt{10}<n+1$,则$n=$
(2)若$n-1<\sqrt{a}<n$,$n<\sqrt{b}<n+1$,则满足条件的$a$的个数总比$b$的个数少
(1)若$n<\sqrt{10}<n+1$,则$n=$
3
;(2)若$n-1<\sqrt{a}<n$,$n<\sqrt{b}<n+1$,则满足条件的$a$的个数总比$b$的个数少
2
。
答案:
(1)3;
(2)2
(1)3;
(2)2
8.小李同学探索$\sqrt{86}$的近似值的过程如下:
因为面积为86的正方形的边长是$\sqrt{86}$,且$9<\sqrt{86}<10$,所以设$\sqrt{86}=9+x$,其中$0<x<1$,画出示意图如图所示。根据示意图,可得图中最大的正方形的面积为$81+2×9x+x^2$,又因为最大的正方形的面积为86,所以$81+2×9x+x^2=86$。当$x^2<1$时,可忽略$x^2$,得$81+18x\approx86$,解得$x\approx0.28$,所以$\sqrt{86}\approx9.28$。
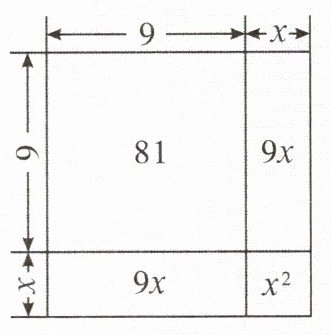
(1)$\sqrt{157}$的整数部分的值为
(2)仿照上述方法,探究$\sqrt{157}$的近似值(结果精确到0.01)。
(答题要求:画出示意图,标明数据,并写出求解过程)
因为面积为86的正方形的边长是$\sqrt{86}$,且$9<\sqrt{86}<10$,所以设$\sqrt{86}=9+x$,其中$0<x<1$,画出示意图如图所示。根据示意图,可得图中最大的正方形的面积为$81+2×9x+x^2$,又因为最大的正方形的面积为86,所以$81+2×9x+x^2=86$。当$x^2<1$时,可忽略$x^2$,得$81+18x\approx86$,解得$x\approx0.28$,所以$\sqrt{86}\approx9.28$。

(1)$\sqrt{157}$的整数部分的值为
12
;(2)仿照上述方法,探究$\sqrt{157}$的近似值(结果精确到0.01)。
(答题要求:画出示意图,标明数据,并写出求解过程)
答案:
(1)12;
(2)因为面积为157的正方形的边长是$\sqrt{157}$,且$12<\sqrt{157}<13$,所以设$\sqrt{157}=12+y$,其中$0<y<1$,画出示示意图如图所示,根据示意图,可得图中最大的正方形的面积为$144+2×12y+y^{2}$,又因为最大的正方形的面积为157,所以$144+2×12y+y^{2}=157$。当$y^{2}<1$时,可忽略$y^{2}$,得$144+24y\approx157$,解得$y\approx0.54$,所以$\sqrt{157}\approx12.54$。
(1)12;
(2)因为面积为157的正方形的边长是$\sqrt{157}$,且$12<\sqrt{157}<13$,所以设$\sqrt{157}=12+y$,其中$0<y<1$,画出示示意图如图所示,根据示意图,可得图中最大的正方形的面积为$144+2×12y+y^{2}$,又因为最大的正方形的面积为157,所以$144+2×12y+y^{2}=157$。当$y^{2}<1$时,可忽略$y^{2}$,得$144+24y\approx157$,解得$y\approx0.54$,所以$\sqrt{157}\approx12.54$。

查看更多完整答案,请扫码查看


