第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
【对点训练2】铺一间面积为$60\ {m^{2}}$的教室的地面,至少需要用大小完全相同的$240$块正方形地板砖,每块地板砖的边长是多少?(地板砖可切割)
答案:
解设每块地板砖的边长为$x$m,由题意,得$240x^{2}=60$,即$x^{2}=0.25$。所以$x=\sqrt{0.25}=0.5$。所以,每块地板砖的边长为0.5m。
1.$100$的算术平方根是(
A.$-10$
B.$10$
C.$\pm10$
D.$\sqrt{10}$
B
)。A.$-10$
B.$10$
C.$\pm10$
D.$\sqrt{10}$
答案:
1.B
2.一个数的算术平方根是$3$,则这个数是(
A.$\sqrt{3}$
B.$9$
C.$\pm\sqrt{3}$
D.$\pm9$
B
)。A.$\sqrt{3}$
B.$9$
C.$\pm\sqrt{3}$
D.$\pm9$
答案:
2.B
3.计算$\sqrt{(-2)^{2}}$等于(
A.$\pm2$
B.$2$
C.$4$
D.$\sqrt{2}$
B
)。A.$\pm2$
B.$2$
C.$4$
D.$\sqrt{2}$
答案:
3.B
4.一块面积为$5\ {m^{2}}$的正方形桌布,其边长为
$\sqrt{5}$m
。
答案:
4.$\sqrt{5}$m
5.若单项式$2x^{m}y^{3}$与$3xy^{m+n}$是同类项,则$\sqrt{2m+n}$的值为
2
。
答案:
5.2
6.已知$(x - 2\sqrt{3})^{2}+|y+2|=0$,求$x^{2}-2y$的算术平方根。
答案:
6.解因为$(x - 2\sqrt{3})^{2}+\vert y + 2\vert=0$,所以$x - 2\sqrt{3}=0,y + 2=0$,所以$x=2\sqrt{3},y=-2$,所以$x^{2}-2y=(2\sqrt{3})^{2}-2×(-2)=16$。因为16的算术平方根是4,所以$x^{2}-2y$的算术平方根为4。
7.下图是一个数值转换器,当输入$x$的值为$9$时,输出$y$的值为(
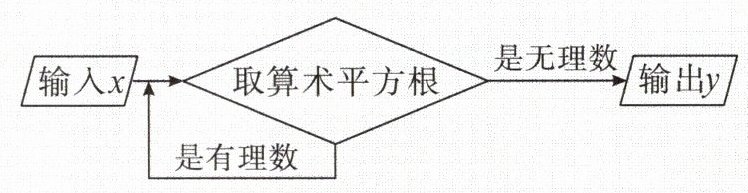
A.$3$
B.$-\sqrt{3}$
C.$\sqrt{3}$
D.$-3$
C
)。
A.$3$
B.$-\sqrt{3}$
C.$\sqrt{3}$
D.$-3$
答案:
7.C
8.若$x$是$\sqrt{81}$的算术平方根,则$x=$
3
。
答案:
8.3
9.某小区准备修建一个面积为$75\ {m^{2}}$的花坛,甲、乙两个工程队给出如下两个施工方案。
甲:花坛为长方形,且长与宽的比为$3:1$。
乙:花坛为正方形。
(1)求长方形花坛的宽;
(2)淇淇说:“正方形花坛的边长肯定比长方形花坛的宽长$3\ {m}$。”请你判断淇淇的说法是否正确,并通过计算说明。
甲:花坛为长方形,且长与宽的比为$3:1$。
乙:花坛为正方形。

(1)求长方形花坛的宽;
(2)淇淇说:“正方形花坛的边长肯定比长方形花坛的宽长$3\ {m}$。”请你判断淇淇的说法是否正确,并通过计算说明。
答案:
9.解
(1)设长方形花坛的宽为$x$m,则长为$3x$m,由题意得$x\cdot3x=3x^{2}=75$,所以$x^{2}=25$,所以$x=\sqrt{25}=5$,即长方形花坛的宽为5m。
(2)淇淇的说法错误,理由:
由
(1)知长方形花坛的宽为5m,若淇淇的说法正确,正方形花坛的边长为$5 + 3=8(m)$,则正方形花坛的面积为$8^{2}=64m^{2}\neq75m^{2}$,因此假设不成立,即淇淇的说法错误。
(1)设长方形花坛的宽为$x$m,则长为$3x$m,由题意得$x\cdot3x=3x^{2}=75$,所以$x^{2}=25$,所以$x=\sqrt{25}=5$,即长方形花坛的宽为5m。
(2)淇淇的说法错误,理由:
由
(1)知长方形花坛的宽为5m,若淇淇的说法正确,正方形花坛的边长为$5 + 3=8(m)$,则正方形花坛的面积为$8^{2}=64m^{2}\neq75m^{2}$,因此假设不成立,即淇淇的说法错误。
查看更多完整答案,请扫码查看


