《2025年伴你学单元达标测试卷九年级物理上册苏科版》

20. 如图所示是一种塔式起重机上的滑轮组.已知在匀速起吊$900\ kg$的物体时,滑轮组的机械率是$80\%$.($g$取$10\ N/kg$)

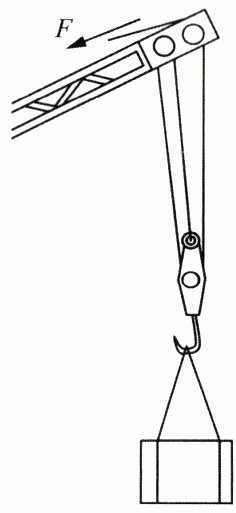
(1) 使物体上升$4\ m$,所做的有用功是多少?
(2) 使物体上升$4\ m$,所做的总功是多少?
(3) 绳端的拉力$F$是多大?

答案： 1. （1）解：
首先求物体的重力$G = mg$，已知$m = 900\ kg$，$g = 10\ N/kg$，则$G=900×10 = 9000\ N$。
有用功公式$W_{有}=Gh$，$h = 4\ m$，所以$W_{有}=9000×4=36000\ J$。
2. （2）解：
由机械效率公式$\eta=\frac{W_{有}}{W_{总}}$，已知$\eta = 80\%=0.8$，$W_{有}=36000\ J$。
则$W_{总}=\frac{W_{有}}{\eta}=\frac{36000}{0.8}=45000\ J$。
3. （3）解：
由图可知$n = 3$，$s = nh$，$h = 4\ m$，所以$s = 3×4 = 12\ m$。
又因为$W_{总}=Fs$，$W_{总}=45000\ J$，$s = 12\ m$。
则$F=\frac{W_{总}}{s}=\frac{45000}{12}=3750\ N$。
综上，（1）有用功是$36000\ J$；（2）总功是$45000\ J$；（3）绳端拉力$F$是$3750\ N$。