《2025年伴你学单元达标测试卷九年级物理上册苏科版》

19. (12分)为研究甲、乙两种液体的吸热升温情况,某小组同学用如图所示两套完全相同的装置进行实验探究,两种液体的质量和初温都相同.


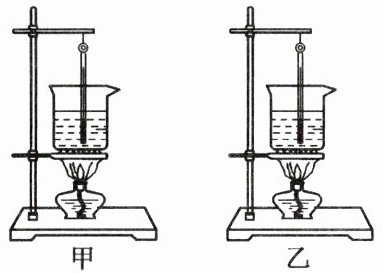
同时加热两种液体,分别记录加热时间和液体温度,数据如表格所示:
(1) 选用两套完全相同的装置分别给甲、乙两种液体加热,这样做的目的是保证加热相同的时间内,两种液体吸收的热量相同;
(2) 加热4分钟后,甲、乙两种液体温度均不再升高,原因是液体达到了沸点;
(3) 根据实验数据,可知:质量相等的甲乙两种液体,升高相等的温度,甲(甲/乙)液体吸收的热量更多;
(4) 另一组同学利用上面的装置研究燃料的热值,除了将两装置中的酒精灯换做燃烧皿,在其中放入等质量的酒精和碎纸片以外,还需做出的调整是两烧杯中换做等质量的同种液体.

答案：
(1) 保证加热相同的时间内,两种液体吸收的热量相同
(2) 液体达到了沸点
(3) 甲
(4) 两烧杯中换做等质量的同种液体

20. (16分)(2024·江苏常州)中国工程师利用焦炉气中的氢气与工业尾气中的二氧化碳,合成液态燃料,作为第19届亚洲运动会主火炬的燃料. 工程师在科普馆用如图所示的装置为同学们演示模拟实验,测量该燃料的热值.
①在空酒精灯内加入适量该液态燃料,得到“燃料灯”;
②在空烧杯内加入$1kg$水,测得水的初温为$31^{\circ}C$,点燃“燃料灯”开始加热;
③当水恰好沸腾时,立即熄灭“燃料灯”,测得“燃料灯”消耗燃料$30g$.
已知实验时气压为1标准大气压,$c_{水}=4.2×10^{3}J/(kg\cdot^{\circ}C)$,用该装置加热水的效率为$42\%$.求:

(1) 此过程中,烧杯内水吸收的热量;
(2) 该液态燃料的热值.

答案： 1. （1）解：
1标准大气压下水的沸点$t = 100^{\circ}C$。
根据热量计算公式$Q_{吸}=c_{水}m_{水}(t - t_{0})$，其中$c_{水}=4.2×10^{3}J/(kg\cdot^{\circ}C)$，$m_{水}=1kg$，$t = 100^{\circ}C$，$t_{0}=31^{\circ}C$。
则$Q_{吸}=4.2×10^{3}J/(kg\cdot^{\circ}C)×1kg×(100 - 31)^{\circ}C$
$=4.2×10^{3}J/(kg\cdot^{\circ}C)×1kg×69^{\circ}C$
$=2.898×10^{5}J$。
2. （2）解：
已知加热水的效率$\eta = 42\%$，由$\eta=\frac{Q_{吸}}{Q_{放}}$可得$Q_{放}=\frac{Q_{吸}}{\eta}$。
把$Q_{吸}=2.898×10^{5}J$，$\eta = 42\%=0.42$代入，得$Q_{放}=\frac{2.898×10^{5}J}{0.42}=6.9×10^{5}J$。
燃料质量$m = 30g=0.03kg$，根据热值公式$q=\frac{Q_{放}}{m}$。
则$q=\frac{6.9×10^{5}J}{0.03kg}=2.3×10^{7}J/kg$。
综上，（1）烧杯内水吸收的热量为$2.898×10^{5}J$；（2）该液态燃料的热值为$2.3×10^{7}J/kg$。