《2025年金学典同步解析与测评贵州人民出版社九年级数学上册人教版》

22. (本题满分 10 分)
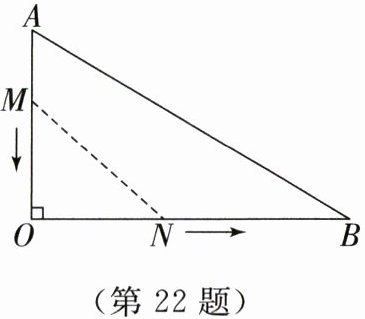
如图,在 $\triangle AOB$ 中,$\angle O = 90^{\circ}$,$AO = 18\ cm$,$BO = 30\ cm$,动点 $M$ 从点 $A$ 开始沿边 $AO$ 以 $1\ cm/s$ 的速度向终点 $O$ 移动,动点 $N$ 从点 $O$ 开始沿边 $OB$ 以 $2\ cm/s$ 的速度向终点 $B$ 移动,一个点到达终点时,另一个点也停止运动. 如果 $M$,$N$ 两点分别从 $A$,$O$ 两点同时出发,设运动时间为 $t$($s$)时四边形 $ABNM$ 的面积为 $S$($cm^{2}$).
(1)求 $S$ 关于 $t$ 的函数关系式,并直接写出 $t$ 的取值范围；
(2)判断 $S$ 有最大值还是有最小值,用配方法求出这个值.

答案： 【解】
(1)由题意，得AM=t,ON=2t，则OM=OA-AM=18-t，所以S=S△AOB-S△MON=1/2×18×30-1/2·(18-t)·2t=t²-18t+270(0＜t≤15).
(2)S=t²-18t+270=t²-18t+81-81+270=(t-9)²+189，因为a=1＞0，所以S有最小值，这个值是189.

23. (本题满分 12 分)
阅读材料：对于任何实数,我们规定符号 $\begin{vmatrix}a&b\\c&d\end{vmatrix} $ 的意义是 $\begin{vmatrix}a&b\\c&d\end{vmatrix} = ad - bc$,例如：$\begin{vmatrix}1&2\\3&4\end{vmatrix} = 1×4 - 2×3 = -2$,$\begin{vmatrix}-2&4\\3&5\end{vmatrix} = (-2)×5 - 4×3 = -22$.
(1)按照这个规定请你计算 $\begin{vmatrix}5&6\\9&3\end{vmatrix} $ 的值；
(2)按照这个规定请你计算：当 $x^{2}-4x + 4 = 0$ 时,$\begin{vmatrix}x + 1&2x\\x - 1&2x - 1\end{vmatrix} $ 的值；
(3)当 $\begin{vmatrix}x + 1&x\\x - 1&2x + 1\end{vmatrix} $ 的值为 $13$ 时,求 $x$ 的值.

答案： 【解】
(1)|5 6| |9 3|=5×3-6×9=-39.
(2)因为x²-4x+4=0，所以(x-2)²=0，解得x=2，所以|x+1 2x| |x-1 2x-1|=(x+1)(2x-1)-2x(x-1)=2x²+x-1-2x²+2x=3x-1=3×2-1=5.
(3)由题意，得|x+1 x| |x-1 2x+1|=13，即(x+1)(2x+1)-x(x-1)=13，整理，得x²+4x-12=0，解得x₁=-6,x₂=2.