2025年金学典同步解析与测评贵州人民出版社九年级数学上册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年金学典同步解析与测评贵州人民出版社九年级数学上册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
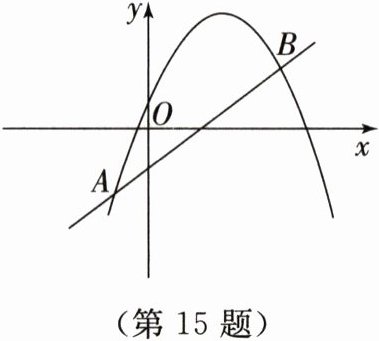
15. 如图,直线 $y = \frac{3}{4}x - m$ 与抛物线 $y = ax^{2}+bx + c$ 交于 $A(-1,-2)$,$B(n,\frac{7}{4})$ 两点,如果 $\frac{3}{4}x - m>ax^{2}+bx + c$,那么 $x$ 的取值范围是______.

答案:
x<-1或x>4
16. 飞机着陆后滑行的距离 $s$(单位:$m$)关于滑行的时间 $t$(单位:$s$)的函数解析式是 $s = 76t - 2t^{2}$,则飞机着陆后从开始滑行到完全停止所用的时间是______ $s$.
答案:
19
17. (本题满分 12 分)
解下列方程:
(1)$3x^{2}+3x - 1 = 0$;
(2)$3(x - 2)^{2}= x^{2}-4$;
(3)$(x + 2)^{2}-3(x + 2)= 0$.
解下列方程:
(1)$3x^{2}+3x - 1 = 0$;
(2)$3(x - 2)^{2}= x^{2}-4$;
(3)$(x + 2)^{2}-3(x + 2)= 0$.
答案:
【解】
(1)3x²+3x - 1 = 0,因为a=3,b=3,c=-1,即Δ=3²-4×3×(-1)=9+12=21>0,得x=(-3±√21)/(2×3)=(-3±√21)/6,所以x₁=(-3+√21)/6,x₂=(-3-√21)/6.
(2)3(x - 2)²=x²-4,3(x-2)²-(x-2)(x+2)=0,(x-2)[3(x-2)-(x+2)]=0,(x-2)(2x-8)=0,得x-2=0或2x-8=0,所以x₁=2,x₂=4.
(3)(x + 2)²-3(x + 2)= 0,(x+2)(x+2-3)=0,(x+2)(x-1)=0,得x+2=0或x-1=0,所以x₁=-2,x₂=1.
(1)3x²+3x - 1 = 0,因为a=3,b=3,c=-1,即Δ=3²-4×3×(-1)=9+12=21>0,得x=(-3±√21)/(2×3)=(-3±√21)/6,所以x₁=(-3+√21)/6,x₂=(-3-√21)/6.
(2)3(x - 2)²=x²-4,3(x-2)²-(x-2)(x+2)=0,(x-2)[3(x-2)-(x+2)]=0,(x-2)(2x-8)=0,得x-2=0或2x-8=0,所以x₁=2,x₂=4.
(3)(x + 2)²-3(x + 2)= 0,(x+2)(x+2-3)=0,(x+2)(x-1)=0,得x+2=0或x-1=0,所以x₁=-2,x₂=1.
查看更多完整答案,请扫码查看


