2025年金学典同步解析与测评贵州人民出版社九年级数学上册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年金学典同步解析与测评贵州人民出版社九年级数学上册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
18. (本题满分 10 分)
如图,在平面直角坐标系中,已知 $ \triangle ABC $ 的三个顶点的坐标分别为 $ A(-1,1) $,$ B(-4,0) $,$ C(-2,2) $. 将 $ \triangle ABC $ 绕原点 $ O $ 顺时针旋转 $ 90^{\circ} $ 后得到 $ \triangle A_{1}B_{1}C_{1} $.
(1)请写出 $ A_{1} $,$ B_{1} $,$ C_{1} $ 三点的坐标:$ A_{1} $ ______,$ B_{1} $ ______,$ C_{1} $ ______;
(2)求点 $ B $ 旋转到点 $ B_{1} $ 的弧长.
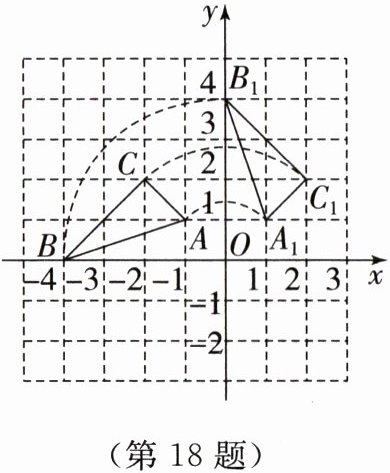
如图,在平面直角坐标系中,已知 $ \triangle ABC $ 的三个顶点的坐标分别为 $ A(-1,1) $,$ B(-4,0) $,$ C(-2,2) $. 将 $ \triangle ABC $ 绕原点 $ O $ 顺时针旋转 $ 90^{\circ} $ 后得到 $ \triangle A_{1}B_{1}C_{1} $.
(1)请写出 $ A_{1} $,$ B_{1} $,$ C_{1} $ 三点的坐标:$ A_{1} $ ______,$ B_{1} $ ______,$ C_{1} $ ______;
(2)求点 $ B $ 旋转到点 $ B_{1} $ 的弧长.

答案:
【解】
(1)$(1,1)$ $(0,4)$ $(2,2)$
(2)由图知点$B$旋转到点$B_{1}$的弧长所对的圆心角是$90^{\circ}$,$OB=4$,所以点$B$旋转到点$B_{1}$的弧长$=\frac{90\pi×4}{180}=2\pi$.
(1)$(1,1)$ $(0,4)$ $(2,2)$
(2)由图知点$B$旋转到点$B_{1}$的弧长所对的圆心角是$90^{\circ}$,$OB=4$,所以点$B$旋转到点$B_{1}$的弧长$=\frac{90\pi×4}{180}=2\pi$.
19. (本题满分 10 分)
已知二次函数 $ y = -\frac{1}{2}(x - h)^{2}+k $ 的部分图象如图,$ A $ 为抛物线顶点.
(1)写出二次函数的解析式;
(2)若抛物线上有两点 $ B(x_{1},y_{1}) $,$ C(x_{2},y_{2}) $,且 $ -1 \lt x_{1} \lt x_{2} $,则 $ y_{1} $ ______ $ y_{2} $(选填“$ \gt $”“$ \lt $”或“$ = $”);
(3)观察图象,直接写出当 $ y \gt 0 $ 时,$ x $ 的取值范围.
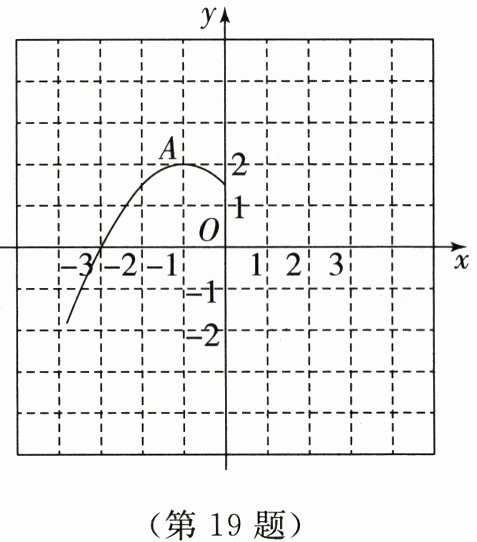
已知二次函数 $ y = -\frac{1}{2}(x - h)^{2}+k $ 的部分图象如图,$ A $ 为抛物线顶点.
(1)写出二次函数的解析式;
(2)若抛物线上有两点 $ B(x_{1},y_{1}) $,$ C(x_{2},y_{2}) $,且 $ -1 \lt x_{1} \lt x_{2} $,则 $ y_{1} $ ______ $ y_{2} $(选填“$ \gt $”“$ \lt $”或“$ = $”);
(3)观察图象,直接写出当 $ y \gt 0 $ 时,$ x $ 的取值范围.

答案:
【解】
(1)根据图示知,抛物线顶点坐标是$(-1,2)$,则该抛物线的解析式是$y=-\frac{1}{2}(x+1)^{2}+2$.
(2)$>$
(3)由抛物线$y=-\frac{1}{2}(x+1)^{2}+2$的对称轴是直线$x=-1$知,抛物线与$x$轴的另一个交点的坐标是$(1,0)$,所以当$y>0$时,$x$的取值范围是$-3< x<1$.
(1)根据图示知,抛物线顶点坐标是$(-1,2)$,则该抛物线的解析式是$y=-\frac{1}{2}(x+1)^{2}+2$.
(2)$>$
(3)由抛物线$y=-\frac{1}{2}(x+1)^{2}+2$的对称轴是直线$x=-1$知,抛物线与$x$轴的另一个交点的坐标是$(1,0)$,所以当$y>0$时,$x$的取值范围是$-3< x<1$.
查看更多完整答案,请扫码查看


