2025年金学典同步解析与测评贵州人民出版社九年级数学上册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年金学典同步解析与测评贵州人民出版社九年级数学上册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
12. 二次函数 $ y = ax^{2}+bx + c $ 的图象如图. 则下列结论:① $ ac \lt 0 $;② $ 3a + c = 0 $;③ $ 4ac - b^{2} \lt 0 $;④当 $ x \gt -1 $ 时,$ y $ 随 $ x $ 的增大而减小,其中正确的有( ).
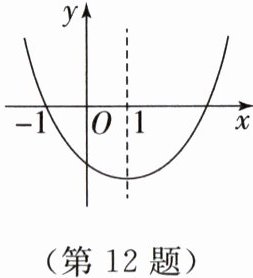
A.4 个
B.3 个
C.2 个
D.1 个

A.4 个
B.3 个
C.2 个
D.1 个
答案:
B
13. 若关于 $ x $ 的一元二次方程 $ x^{2} - 4x + 2k = 0 $ 有两个相等的实数根,则 $ k $ 的值为 ______.
答案:
2
14. 已知点 $ P_{1}(a - 1,1) $ 和点 $ P_{2}(2,b - 1) $ 关于原点对称,则 $ (a + b)^{2025} $ 的值为 ______.
答案:
-1
15. 如图,从一张腰长为 $ \sqrt{2}\ cm $ 的等腰直角三角形铁皮 $ OAB $ 中剪出一个最大的扇形 $ OCD $,用剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面半径为 ______ $ cm $.
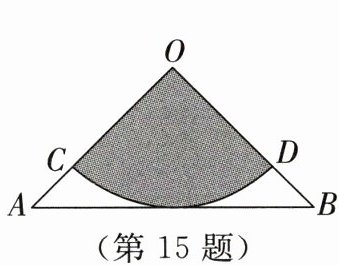

答案:
$\frac{1}{4}$
16. 如图,$ \triangle ABC $ 的内切圆与三边分别相切于点 $ D $,$ E $,$ F $. 若 $ \angle B = 50^{\circ} $,则 $ \angle EDF = $ ______.
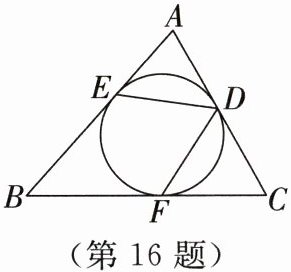

答案:
$65^{\circ}$
17. (本题满分 12 分)
(1)解方程:$ x^{2} - 2\sqrt{5}x + 2 = 0 $.
(2)若 $ x = -1 $ 是关于 $ x $ 的一元二次方程 $ (m - 1)x^{2} - x - 2 = 0 $ 的一个根,求 $ m $ 的值及另一个根.
(1)解方程:$ x^{2} - 2\sqrt{5}x + 2 = 0 $.
(2)若 $ x = -1 $ 是关于 $ x $ 的一元二次方程 $ (m - 1)x^{2} - x - 2 = 0 $ 的一个根,求 $ m $ 的值及另一个根.
答案:
【解】
(1)$a=1$,$b=-2\sqrt{5}$,$c=2$,即$\Delta =b^{2}-4ac=(-2\sqrt{5})^{2}-4×1×2=12>0$.得$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}=\frac{2\sqrt{5}\pm\sqrt{12}}{2}$.所以$x_{1}=\sqrt{5}+\sqrt{3}$,$x_{2}=\sqrt{5}-\sqrt{3}$.
(2)将$x=-1$代入方程,得$m-1+1-2=0$,解得$m=2$,所以原方程为$x^{2}-x-2=(x+1)(x-2)=0$,解得$x_{1}=-1$,$x_{2}=2$.所以$m$的值为$2$,方程的另一个根为$2$.
(1)$a=1$,$b=-2\sqrt{5}$,$c=2$,即$\Delta =b^{2}-4ac=(-2\sqrt{5})^{2}-4×1×2=12>0$.得$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}=\frac{2\sqrt{5}\pm\sqrt{12}}{2}$.所以$x_{1}=\sqrt{5}+\sqrt{3}$,$x_{2}=\sqrt{5}-\sqrt{3}$.
(2)将$x=-1$代入方程,得$m-1+1-2=0$,解得$m=2$,所以原方程为$x^{2}-x-2=(x+1)(x-2)=0$,解得$x_{1}=-1$,$x_{2}=2$.所以$m$的值为$2$,方程的另一个根为$2$.
查看更多完整答案,请扫码查看


