2025年新坐标同步练习高中数学A版选择性必修第三册人教版青海专用
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新坐标同步练习高中数学A版选择性必修第三册人教版青海专用 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第86页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
三 样本相关系数
1. 样本相关系数计算公式
对于变量 $ x $ 和变量 $ y $,设经过随机抽样获得的成对样本数据为 $ (x_{1}, y_{1}) $,$ (x_{2}, y_{2}) $,…$ $,$ (x_{n}, y_{n}) $,其中 $ x_{1} $,$ x_{2} $,…$ $,$ x_{n} $ 和 $ y_{1} $,$ y_{2} $,…$ $,$ y_{n} $ 的均值分别为 $ \overline{x} $ 和 $ \overline{y} $,则
$r= \frac{\sum_{i = 1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})}{\sqrt{\sum_{i = 1}^{n}(x_{i}-\overline{x})^{2}}\sqrt{\sum_{i = 1}^{n}(y_{i}-\overline{y})^{2}}}= \frac{\sum_{i = 1}^{n}x_{i}y_{i}-n\overline{x}\,\overline{y}}{\sqrt{\sum_{i = 1}^{n}x_{i}^{2}-n\overline{x}^{2}}\sqrt{\sum_{i = 1}^{n}y_{i}^{2}-n\overline{y}^{2}}}.$
称 $ r $ 为变量 $ x $ 和变量 $ y $ 的样本相关系数。
2. 样本相关系数的性质
(1)样本相关系数 $ r $ 的取值范围为
(2)当 $ r>0 $ 时,称成对样本数据正相关;当 $ r<0 $ 时,称成对样本数据负相关;
(3)$ |r| $ 越接近 1,成对样本数据的线性相关程度越强;$ |r| $ 越接近 0,成对样本数据的线性相关程度越弱。
1. 样本相关系数计算公式
对于变量 $ x $ 和变量 $ y $,设经过随机抽样获得的成对样本数据为 $ (x_{1}, y_{1}) $,$ (x_{2}, y_{2}) $,…$ $,$ (x_{n}, y_{n}) $,其中 $ x_{1} $,$ x_{2} $,…$ $,$ x_{n} $ 和 $ y_{1} $,$ y_{2} $,…$ $,$ y_{n} $ 的均值分别为 $ \overline{x} $ 和 $ \overline{y} $,则
$r= \frac{\sum_{i = 1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})}{\sqrt{\sum_{i = 1}^{n}(x_{i}-\overline{x})^{2}}\sqrt{\sum_{i = 1}^{n}(y_{i}-\overline{y})^{2}}}= \frac{\sum_{i = 1}^{n}x_{i}y_{i}-n\overline{x}\,\overline{y}}{\sqrt{\sum_{i = 1}^{n}x_{i}^{2}-n\overline{x}^{2}}\sqrt{\sum_{i = 1}^{n}y_{i}^{2}-n\overline{y}^{2}}}.$
称 $ r $ 为变量 $ x $ 和变量 $ y $ 的样本相关系数。
2. 样本相关系数的性质
(1)样本相关系数 $ r $ 的取值范围为
[-1,1]
;(2)当 $ r>0 $ 时,称成对样本数据正相关;当 $ r<0 $ 时,称成对样本数据负相关;
(3)$ |r| $ 越接近 1,成对样本数据的线性相关程度越强;$ |r| $ 越接近 0,成对样本数据的线性相关程度越弱。
答案:
[-1,1]
1. 对四组不同数据进行统计,获得如图所示的散点图,对它们的样本相关系数进行比较,正确的是(
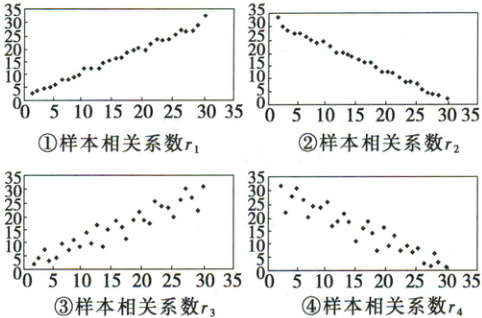
A.$ r_{2}<r_{4}<0<r_{3}<r_{1} $
B.$ r_{4}<r_{2}<0<r_{1}<r_{3} $
C.$ r_{4}<r_{2}<0<r_{3}<r_{1} $
D.$ r_{2}<r_{4}<0<r_{1}<r_{3} $
A
)
A.$ r_{2}<r_{4}<0<r_{3}<r_{1} $
B.$ r_{4}<r_{2}<0<r_{1}<r_{3} $
C.$ r_{4}<r_{2}<0<r_{3}<r_{1} $
D.$ r_{2}<r_{4}<0<r_{1}<r_{3} $
答案:
A
2. 某唱片公司想了解唱片费用 $ x $(单位:十万元)与唱片销售量 $ y $(单位:千张)之间的关系,现从其所发行的唱片中随机抽取了 10 张,得到如下的资料:
$\sum_{i = 1}^{10}x_{i}= 28,\sum_{i = 1}^{10}x_{i}^{2}= 303.4,\sum_{i = 1}^{10}y_{i}= 75,\sum_{i = 1}^{10}y_{i}^{2}= 598.5,\sum_{i = 1}^{10}x_{i}y_{i}= 237,$
则 $ y $ 与 $ x $ 的样本相关系数 $ r = $
$\sum_{i = 1}^{10}x_{i}= 28,\sum_{i = 1}^{10}x_{i}^{2}= 303.4,\sum_{i = 1}^{10}y_{i}= 75,\sum_{i = 1}^{10}y_{i}^{2}= 598.5,\sum_{i = 1}^{10}x_{i}y_{i}= 237,$
则 $ y $ 与 $ x $ 的样本相关系数 $ r = $
0.3
。
答案:
0.3
例2
(对接教材例1)科研人员在对人体脂肪含量 $ y $ 和年龄 $ x $ 之间关系的研究中,获得了一些年龄和脂肪含量的简单随机样本数据,如下表:

根据上表的数据得到如下的散点图。
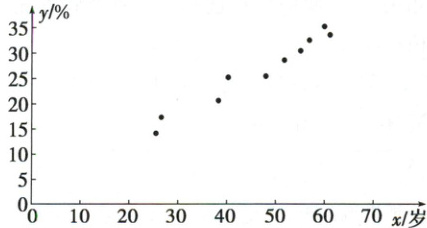
(1)求 $ \overline{x} $;
(2)计算样本相关系数(精确到 0.01),并刻画它们的线性相关程度。
参考数据:$ \overline{y}= 27 $,$ \sum_{i = 1}^{10}x_{i}y_{i}= 13527.8 $,$ \sum_{i = 1}^{10}x_{i}^{2}= 23638 $,$ \sum_{i = 1}^{10}y_{i}^{2}= 7759.6 $,$ \sqrt{43}\approx6.56 $,$ \sqrt{2935}\approx54.18 $,
参考公式:样本相关系数
$r= \frac{\sum_{i = 1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})}{\sqrt{\sum_{i = 1}^{n}(x_{i}-\overline{x})^{2}}\sqrt{\sum_{i = 1}^{n}(y_{i}-\overline{y})^{2}}}= \frac{\sum_{i = 1}^{n}x_{i}y_{i}-n\overline{x}\,\overline{y}}{\sqrt{\sum_{i = 1}^{n}x_{i}^{2}-n\overline{x}^{2}}\sqrt{\sum_{i = 1}^{n}y_{i}^{2}-n\overline{y}^{2}}}.$
(对接教材例1)科研人员在对人体脂肪含量 $ y $ 和年龄 $ x $ 之间关系的研究中,获得了一些年龄和脂肪含量的简单随机样本数据,如下表:

根据上表的数据得到如下的散点图。

(1)求 $ \overline{x} $;
(2)计算样本相关系数(精确到 0.01),并刻画它们的线性相关程度。
参考数据:$ \overline{y}= 27 $,$ \sum_{i = 1}^{10}x_{i}y_{i}= 13527.8 $,$ \sum_{i = 1}^{10}x_{i}^{2}= 23638 $,$ \sum_{i = 1}^{10}y_{i}^{2}= 7759.6 $,$ \sqrt{43}\approx6.56 $,$ \sqrt{2935}\approx54.18 $,
参考公式:样本相关系数
$r= \frac{\sum_{i = 1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})}{\sqrt{\sum_{i = 1}^{n}(x_{i}-\overline{x})^{2}}\sqrt{\sum_{i = 1}^{n}(y_{i}-\overline{y})^{2}}}= \frac{\sum_{i = 1}^{n}x_{i}y_{i}-n\overline{x}\,\overline{y}}{\sqrt{\sum_{i = 1}^{n}x_{i}^{2}-n\overline{x}^{2}}\sqrt{\sum_{i = 1}^{n}y_{i}^{2}-n\overline{y}^{2}}}.$
(1)$\overline{x}=\frac{1}{10}×(26+27+39+41+49+53+56+58+60+61)=47$.
(2)$r=\frac{\sum_{i = 1}^{10}x_{i}y_{i}-10\overline{x}\,\overline{y}}{\sqrt{\sum_{i = 1}^{10}x_{i}^{2}-10\overline{x}^{2}}\sqrt{\sum_{i = 1}^{10}y_{i}^{2}-10\overline{y}^{2}}}=\frac{13527.8-10×47×27}{\sqrt{23638-10×47^{2}}×\sqrt{7759.6-10×27^{2}}}=\frac{13527.8-12690}{\sqrt{23638-22090}×\sqrt{7759.6-7290}}=\frac{837.8}{\sqrt{1548}×\sqrt{469.6}}=\frac{8378}{6\sqrt{43}×4\sqrt{2935}}\approx\frac{8378}{6×6.56×4×54.18}\approx0.98$.
由样本相关系数$r\approx0.98$,可以推断人体脂肪含量和年龄的线性相关程度很强.
(2)$r=\frac{\sum_{i = 1}^{10}x_{i}y_{i}-10\overline{x}\,\overline{y}}{\sqrt{\sum_{i = 1}^{10}x_{i}^{2}-10\overline{x}^{2}}\sqrt{\sum_{i = 1}^{10}y_{i}^{2}-10\overline{y}^{2}}}=\frac{13527.8-10×47×27}{\sqrt{23638-10×47^{2}}×\sqrt{7759.6-10×27^{2}}}=\frac{13527.8-12690}{\sqrt{23638-22090}×\sqrt{7759.6-7290}}=\frac{837.8}{\sqrt{1548}×\sqrt{469.6}}=\frac{8378}{6\sqrt{43}×4\sqrt{2935}}\approx\frac{8378}{6×6.56×4×54.18}\approx0.98$.
由样本相关系数$r\approx0.98$,可以推断人体脂肪含量和年龄的线性相关程度很强.
答案:
(1)$\overline{x}=\frac{1}{10}×(26+27+39+41+49+53+56+58+60+61)=47$.
(2)$r=\frac{\sum_{i = 1}^{10}x_{i}y_{i}-10\overline{x}\,\overline{y}}{\sqrt{\sum_{i = 1}^{10}x_{i}^{2}-10\overline{x}^{2}}\sqrt{\sum_{i = 1}^{10}y_{i}^{2}-10\overline{y}^{2}}}=\frac{13527.8-10×47×27}{\sqrt{23638-10×47^{2}}×\sqrt{7759.6-10×27^{2}}}=\frac{13527.8-12690}{\sqrt{23638-22090}×\sqrt{7759.6-7290}}=\frac{837.8}{\sqrt{1548}×\sqrt{469.6}}=\frac{8378}{6\sqrt{43}×4\sqrt{2935}}\approx\frac{8378}{6×6.56×4×54.18}\approx0.98$.
由样本相关系数$r\approx0.98$,可以推断人体脂肪含量和年龄的线性相关程度很强.
(2)$r=\frac{\sum_{i = 1}^{10}x_{i}y_{i}-10\overline{x}\,\overline{y}}{\sqrt{\sum_{i = 1}^{10}x_{i}^{2}-10\overline{x}^{2}}\sqrt{\sum_{i = 1}^{10}y_{i}^{2}-10\overline{y}^{2}}}=\frac{13527.8-10×47×27}{\sqrt{23638-10×47^{2}}×\sqrt{7759.6-10×27^{2}}}=\frac{13527.8-12690}{\sqrt{23638-22090}×\sqrt{7759.6-7290}}=\frac{837.8}{\sqrt{1548}×\sqrt{469.6}}=\frac{8378}{6\sqrt{43}×4\sqrt{2935}}\approx\frac{8378}{6×6.56×4×54.18}\approx0.98$.
由样本相关系数$r\approx0.98$,可以推断人体脂肪含量和年龄的线性相关程度很强.
查看更多完整答案,请扫码查看


