《2025年新坐标同步练习高中数学A版选择性必修第三册人教版青海专用》

典例 甲、乙两人去某公司应聘面试. 该公司的面试方案为：应聘者从 6 道备选题中一次性随机抽取 3 道题,按照答对题目的个数为标准进行筛选. 已知 6 道备选题中应聘者甲有 4 道题能正确完成,2 道题不能完成；应聘者乙每题正确完成的概率都是 $ \frac{2}{3} $,且每题正确完成与否互不影响.
(1) 分别求甲、乙两人正确完成面试题数的分布列,并计算其均值；
(2) 请分析比较甲、乙两人谁的面试通过的可能性较大？
【解】（1）设X为甲正确完成面试题的数量，Y为乙正确完成面试题的数量，依题意可得X服从超几何分布，所以$P(X=1)=\frac{C_{4}^{1}C_{2}^{2}}{C_{6}^{3}}=\frac{1}{5}$，$P(X=2)=\frac{C_{4}^{2}C_{2}^{1}}{C_{6}^{3}}=\frac{3}{5}$，$P(X=3)=\frac{C_{4}^{3}C_{2}^{0}}{C_{6}^{3}}=\frac{1}{5}$，所以X的分布列为
X
1
2
3
P
$\frac{1}{5}$
$\frac{3}{5}$
$\frac{1}{5}$
所以$E(X)=1×\frac{1}{5}+2×\frac{3}{5}+3×\frac{1}{5}=2$。
$Y\sim B(3,\frac{2}{3})$，所以$P(Y=0)=C_{3}^{0}(\frac{2}{3})^{0}(\frac{1}{3})^{3}=\frac{1}{27}$，$P(Y=1)=C_{3}^{1}×\frac{2}{3}×(\frac{1}{3})^{2}=\frac{2}{9}$，$P(Y=2)=C_{3}^{2}(\frac{2}{3})^{2}×\frac{1}{3}=\frac{4}{9}$，$P(Y=3)=C_{3}^{3}(\frac{2}{3})^{3}×(\frac{1}{3})^{0}=\frac{8}{27}$，所以Y的分布列为
Y
0
1
2
3
P
$\frac{1}{27}$
$\frac{2}{9}$
$\frac{4}{9}$
$\frac{8}{27}$
所以$E(Y)=0×\frac{1}{27}+1×\frac{2}{9}+2×\frac{4}{9}+3×\frac{8}{27}=2$。
（2）由（1）得$E(X)=E(Y)$，$D(X)=(1-2)^{2}×\frac{1}{5}+(2-2)^{2}×\frac{3}{5}+(3-2)^{2}×\frac{1}{5}=\frac{2}{5}$，$D(Y)=np(1-p)=3×\frac{2}{3}×\frac{1}{3}=\frac{2}{3}$，因为$D(X)＜D(Y)$，所以甲发挥的稳定性更强，则甲通过面试的可能性较大。

答案： 【解】（1）设X为甲正确完成面试题的数量，Y为乙正确完成面试题的数量，依题意可得X服从超几何分布，所以$P(X=1)=\frac{C_{4}^{1}C_{2}^{2}}{C_{6}^{3}}=\frac{1}{5}$，$P(X=2)=\frac{C_{4}^{2}C_{2}^{1}}{C_{6}^{3}}=\frac{3}{5}$，$P(X=3)=\frac{C_{4}^{3}C_{2}^{0}}{C_{6}^{3}}=\frac{1}{5}$，所以X的分布列为
X
1
2
3
P
$\frac{1}{5}$
$\frac{3}{5}$
$\frac{1}{5}$
所以$E(X)=1×\frac{1}{5}+2×\frac{3}{5}+3×\frac{1}{5}=2$。
$Y\sim B(3,\frac{2}{3})$，所以$P(Y=0)=C_{3}^{0}(\frac{2}{3})^{0}(\frac{1}{3})^{3}=\frac{1}{27}$，$P(Y=1)=C_{3}^{1}×\frac{2}{3}×(\frac{1}{3})^{2}=\frac{2}{9}$，$P(Y=2)=C_{3}^{2}(\frac{2}{3})^{2}×\frac{1}{3}=\frac{4}{9}$，$P(Y=3)=C_{3}^{3}(\frac{2}{3})^{3}×(\frac{1}{3})^{0}=\frac{8}{27}$，所以Y的分布列为
Y
0
1
2
3
P
$\frac{1}{27}$
$\frac{2}{9}$
$\frac{4}{9}$
$\frac{8}{27}$
所以$E(Y)=0×\frac{1}{27}+1×\frac{2}{9}+2×\frac{4}{9}+3×\frac{8}{27}=2$。
（2）由（1）得$E(X)=E(Y)$，$D(X)=(1-2)^{2}×\frac{1}{5}+(2-2)^{2}×\frac{3}{5}+(3-2)^{2}×\frac{1}{5}=\frac{2}{5}$，$D(Y)=np(1-p)=3×\frac{2}{3}×\frac{1}{3}=\frac{2}{3}$，因为$D(X)＜D(Y)$，所以甲发挥的稳定性更强，则甲通过面试的可能性较大。

1. 在一个袋中装有质地大小一样的 6 个黑球,4 个白球,现从中任取 4 个小球,设取的 4 个小球中白球的个数为 $ X $,则下列结论正确的是(C)
A.$ P(X = 1) = \frac{2}{5} $
B.随机变量 $ X $ 服从二项分布
C.随机变量 $ X $ 服从超几何分布
D.$ E(X) = \frac{8}{3} $

答案： 选C。由题意知随机变量X服从超几何分布，故B错误，C正确；X的可能取值为0，1，2，3，4，则$P(X=0)=\frac{C_{4}^{0}C_{6}^{4}}{C_{10}^{4}}=\frac{1}{14}$，$P(X=1)=\frac{C_{4}^{1}C_{6}^{3}}{C_{10}^{4}}=\frac{8}{21}$，$P(X=2)=\frac{C_{4}^{2}C_{6}^{2}}{C_{10}^{4}}=\frac{3}{7}$，$P(X=3)=\frac{C_{4}^{3}C_{6}^{1}}{C_{10}^{4}}=\frac{4}{35}$，$P(X=4)=\frac{C_{4}^{4}C_{6}^{0}}{C_{10}^{4}}=\frac{1}{210}$，所以$E(X)=0×\frac{1}{14}+1×\frac{8}{21}+2×\frac{3}{7}+3×\frac{4}{35}+4×\frac{1}{210}=\frac{8}{5}$，故A，D错误。故选C。

2. 一个盒子里有大小、形状均相同的 1 个红球、1 个绿球、4 个黄球,每次拿一个,共拿 3 次,记拿到黄色球的个数为 $ X $. 若取球过程是无放回的,则事件“$ X = 2 $”的概率为$\frac{3}{5}$；若取球过程是有放回的,则 $ E(X) = $2.

答案： $\frac{3}{5}$ 2

3. 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球自由下落,在下落的过程中,小球将遇到黑色障碍物 3 次,最后落入 $ A $ 袋或 $ B $ 袋中,已知小球每次遇到障碍物时,向左、右两边下落的概率分别是 $ \frac{1}{3} $,$ \frac{2}{3} $.

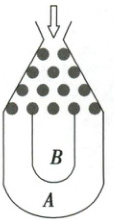
(1) 设M=“小球落入A袋”，N=“小球落入B袋”，则$P(M)=\frac{1}{3}×\frac{1}{3}×\frac{1}{3}+\frac{2}{3}×\frac{2}{3}×\frac{2}{3}=\frac{1}{3}$，所以$P(N)=1-P(M)=1-\frac{1}{3}=\frac{2}{3}$。所以小球落入A袋中的概率为$\frac{1}{3}$，落入B袋中的概率为$\frac{2}{3}$。分别求出小球落入 $ A $ 袋和 $ B $ 袋中的概率；
(2) 在容器的入口处依次放入 4 个小球,记 $ \xi $ 为落入 $ B $ 袋中的小球的个数,求 $ \xi $ 的分布列、均值和方差.

答案： （1）设M=“小球落入A袋”，N=“小球落入B袋”，则$P(M)=\frac{1}{3}×\frac{1}{3}×\frac{1}{3}+\frac{2}{3}×\frac{2}{3}×\frac{2}{3}=\frac{1}{3}$，所以$P(N)=1-P(M)=1-\frac{1}{3}=\frac{2}{3}$。所以小球落入A袋中的概率为$\frac{1}{3}$，落入B袋中的概率为$\frac{2}{3}$。
（2）易知$\xi\sim B(4,\frac{2}{3})$，则ξ的分布列为$P(\xi=k)=C_{4}^{k}(\frac{2}{3})^{k}(\frac{1}{3})^{4-k}(k=0,1,2,3,4)$，故$P(\xi=0)=\frac{1}{81}$，$P(\xi=1)=\frac{8}{81}$，$P(\xi=2)=\frac{24}{81}=\frac{8}{27}$，$P(\xi=3)=\frac{32}{81}$，$P(\xi=4)=\frac{16}{81}$。故ξ的分布列为
ξ
0
1
2
3
4
P
$\frac{1}{81}$
$\frac{8}{81}$
$\frac{8}{27}$
$\frac{32}{81}$
$\frac{16}{81}$
$E(\xi)=4×\frac{2}{3}=\frac{8}{3}$，$D(\xi)=4×\frac{2}{3}×\frac{1}{3}=\frac{8}{9}$。