2025年新坐标同步练习高中数学A版选择性必修第三册人教版青海专用
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新坐标同步练习高中数学A版选择性必修第三册人教版青海专用 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第72页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
三 超几何分布的实际应用及均值
设随机变量X服从超几何分布,则X可以解释为从包含M件次品的N件产品中,不放回地随机抽取n件产品中的次品数. 令p= $\frac{M}{N}$,则p是N件产品的次品率,而$\frac{X}{n}$是抽取的n件产品的次品率,则E(X)= $\frac{nM}{N}$=
设随机变量X服从超几何分布,则X可以解释为从包含M件次品的N件产品中,不放回地随机抽取n件产品中的次品数. 令p= $\frac{M}{N}$,则p是N件产品的次品率,而$\frac{X}{n}$是抽取的n件产品的次品率,则E(X)= $\frac{nM}{N}$=
np
.
答案:
np
例2
近年来,民宿旅游逐渐成为一种热潮,山野乡村的民宿深受广大旅游爱好者的喜爱. 某地区结合当地资源,按照“山上生态做减法、山下产业做加法”的思路,科学有序发展环山文旅康养产业,温泉度假小镇、环山绿道、农家乐提档升级、特色民宿群等一批生态产业项目加快实施. 为了在节假日接待好游客,该地旅游局对本地区各乡村的普通型民宿和品质型民宿进行了调研,随机抽取了10家乡村民宿,统计得到各家的房间数如下表:
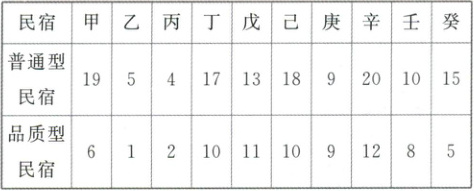
(1) 若旅游局随机从乙、丙2家各选2间民宿进行调研,求选出的4间均为普通型民宿的概率;
(2) 从这10家中随机抽取4家民宿,记其中普通型民宿的房间不低于17间的有X家,求X的分布列和均值.
【解】
(1)设“从乙家选2间民宿,选到的2间民宿为普通型”为事件 A;“从丙家选2间民宿,选到的2间民宿为普通型”为事件 B,所以选出的4间均为普通型民宿的概率为$P(AB)=P(A)P(B)=\frac{C_{4}^{2}}{C_{6}^{2}}×\frac{C_{2}^{2}}{C_{6}^{2}}=\frac{4}{15}$.
(2)由题表得这 10 家民宿中普通型民宿的房间不低于 17 间的有 4 家,则随机变量 X 的可能取值有 0,1,2,3,4.
$P(X = 0)=\frac{C_{4}^{0}C_{6}^{4}}{C_{10}^{4}}=\frac{15}{210}=\frac{1}{14}$,
$P(X = 1)=\frac{C_{4}^{1}C_{6}^{3}}{C_{10}^{4}}=\frac{8}{21}$,
$P(X = 2)=\frac{C_{4}^{2}C_{6}^{2}}{C_{10}^{4}}=\frac{3}{7}$,
$P(X = 3)=\frac{C_{4}^{3}C_{6}^{1}}{C_{10}^{4}}=\frac{4}{35}$,
$P(X = 4)=\frac{C_{4}^{4}C_{6}^{0}}{C_{10}^{4}}=\frac{1}{210}$.
则 X 的分布列为
X 0 1 2 3 4
P $\frac{1}{14}$ $\frac{8}{21}$ $\frac{3}{7}$ $\frac{4}{35}$ $\frac{1}{210}$
方法一:$E(X)=0×\frac{1}{14}+1×\frac{8}{21}+2×\frac{3}{7}+3×\frac{4}{35}+4×\frac{1}{210}=\frac{8}{5}$.
方法二:随机变量 X 服从超几何分布,其中$N = 10,M = 4,n = 4$,所以$E(X)=\frac{nM}{N}=\frac{4×4}{10}=\frac{8}{5}$.
近年来,民宿旅游逐渐成为一种热潮,山野乡村的民宿深受广大旅游爱好者的喜爱. 某地区结合当地资源,按照“山上生态做减法、山下产业做加法”的思路,科学有序发展环山文旅康养产业,温泉度假小镇、环山绿道、农家乐提档升级、特色民宿群等一批生态产业项目加快实施. 为了在节假日接待好游客,该地旅游局对本地区各乡村的普通型民宿和品质型民宿进行了调研,随机抽取了10家乡村民宿,统计得到各家的房间数如下表:

(1) 若旅游局随机从乙、丙2家各选2间民宿进行调研,求选出的4间均为普通型民宿的概率;
(2) 从这10家中随机抽取4家民宿,记其中普通型民宿的房间不低于17间的有X家,求X的分布列和均值.
【解】
(1)设“从乙家选2间民宿,选到的2间民宿为普通型”为事件 A;“从丙家选2间民宿,选到的2间民宿为普通型”为事件 B,所以选出的4间均为普通型民宿的概率为$P(AB)=P(A)P(B)=\frac{C_{4}^{2}}{C_{6}^{2}}×\frac{C_{2}^{2}}{C_{6}^{2}}=\frac{4}{15}$.
(2)由题表得这 10 家民宿中普通型民宿的房间不低于 17 间的有 4 家,则随机变量 X 的可能取值有 0,1,2,3,4.
$P(X = 0)=\frac{C_{4}^{0}C_{6}^{4}}{C_{10}^{4}}=\frac{15}{210}=\frac{1}{14}$,
$P(X = 1)=\frac{C_{4}^{1}C_{6}^{3}}{C_{10}^{4}}=\frac{8}{21}$,
$P(X = 2)=\frac{C_{4}^{2}C_{6}^{2}}{C_{10}^{4}}=\frac{3}{7}$,
$P(X = 3)=\frac{C_{4}^{3}C_{6}^{1}}{C_{10}^{4}}=\frac{4}{35}$,
$P(X = 4)=\frac{C_{4}^{4}C_{6}^{0}}{C_{10}^{4}}=\frac{1}{210}$.
则 X 的分布列为
X 0 1 2 3 4
P $\frac{1}{14}$ $\frac{8}{21}$ $\frac{3}{7}$ $\frac{4}{35}$ $\frac{1}{210}$
方法一:$E(X)=0×\frac{1}{14}+1×\frac{8}{21}+2×\frac{3}{7}+3×\frac{4}{35}+4×\frac{1}{210}=\frac{8}{5}$.
方法二:随机变量 X 服从超几何分布,其中$N = 10,M = 4,n = 4$,所以$E(X)=\frac{nM}{N}=\frac{4×4}{10}=\frac{8}{5}$.
答案:
【解】
(1)设“从乙家选2间民宿,选到的2间民宿为普通型”为事件 A;“从丙家选2间民宿,选到的2间民宿为普通型”为事件 B,所以选出的4间均为普通型民宿的概率为$P(AB)=P(A)P(B)=\frac{C_{4}^{2}}{C_{6}^{2}}×\frac{C_{2}^{2}}{C_{6}^{2}}=\frac{4}{15}$.
(2)由题表得这 10 家民宿中普通型民宿的房间不低于 17 间的有 4 家,则随机变量 X 的可能取值有 0,1,2,3,4.
$P(X = 0)=\frac{C_{4}^{0}C_{6}^{4}}{C_{10}^{4}}=\frac{15}{210}=\frac{1}{14}$,
$P(X = 1)=\frac{C_{4}^{1}C_{6}^{3}}{C_{10}^{4}}=\frac{8}{21}$,
$P(X = 2)=\frac{C_{4}^{2}C_{6}^{2}}{C_{10}^{4}}=\frac{3}{7}$,
$P(X = 3)=\frac{C_{4}^{3}C_{6}^{1}}{C_{10}^{4}}=\frac{4}{35}$,
$P(X = 4)=\frac{C_{4}^{4}C_{6}^{0}}{C_{10}^{4}}=\frac{1}{210}$.
则 X 的分布列为
X 0 1 2 3 4
P $\frac{1}{14}$ $\frac{8}{21}$ $\frac{3}{7}$ $\frac{4}{35}$ $\frac{1}{210}$
方法一:$E(X)=0×\frac{1}{14}+1×\frac{8}{21}+2×\frac{3}{7}+3×\frac{4}{35}+4×\frac{1}{210}=\frac{8}{5}$.
方法二:随机变量 X 服从超几何分布,其中$N = 10,M = 4,n = 4$,所以$E(X)=\frac{nM}{N}=\frac{4×4}{10}=\frac{8}{5}$.
(1)设“从乙家选2间民宿,选到的2间民宿为普通型”为事件 A;“从丙家选2间民宿,选到的2间民宿为普通型”为事件 B,所以选出的4间均为普通型民宿的概率为$P(AB)=P(A)P(B)=\frac{C_{4}^{2}}{C_{6}^{2}}×\frac{C_{2}^{2}}{C_{6}^{2}}=\frac{4}{15}$.
(2)由题表得这 10 家民宿中普通型民宿的房间不低于 17 间的有 4 家,则随机变量 X 的可能取值有 0,1,2,3,4.
$P(X = 0)=\frac{C_{4}^{0}C_{6}^{4}}{C_{10}^{4}}=\frac{15}{210}=\frac{1}{14}$,
$P(X = 1)=\frac{C_{4}^{1}C_{6}^{3}}{C_{10}^{4}}=\frac{8}{21}$,
$P(X = 2)=\frac{C_{4}^{2}C_{6}^{2}}{C_{10}^{4}}=\frac{3}{7}$,
$P(X = 3)=\frac{C_{4}^{3}C_{6}^{1}}{C_{10}^{4}}=\frac{4}{35}$,
$P(X = 4)=\frac{C_{4}^{4}C_{6}^{0}}{C_{10}^{4}}=\frac{1}{210}$.
则 X 的分布列为
X 0 1 2 3 4
P $\frac{1}{14}$ $\frac{8}{21}$ $\frac{3}{7}$ $\frac{4}{35}$ $\frac{1}{210}$
方法一:$E(X)=0×\frac{1}{14}+1×\frac{8}{21}+2×\frac{3}{7}+3×\frac{4}{35}+4×\frac{1}{210}=\frac{8}{5}$.
方法二:随机变量 X 服从超几何分布,其中$N = 10,M = 4,n = 4$,所以$E(X)=\frac{nM}{N}=\frac{4×4}{10}=\frac{8}{5}$.
一盘子中有8个粽子,其中豆沙粽2个,蜜枣粽6个,这两种粽子的外观完全相同,从中随机取出3个.
(1) 求既有豆沙粽又有蜜枣粽的概率;
(2) 设X表示取到豆沙粽的个数,求随机变量X的分布列与均值.
(1) 求既有豆沙粽又有蜜枣粽的概率;
(2) 设X表示取到豆沙粽的个数,求随机变量X的分布列与均值.
解:
(1)依题意,既有豆沙粽又有蜜枣粽的概率为$\frac{C_{2}^{1}C_{6}^{2}+C_{2}^{2}C_{6}^{1}}{C_{8}^{3}}=\frac{9}{14}$.
(2)X 的可能取值为 0,1,2.
$P(X = 0)=\frac{C_{2}^{0}C_{6}^{3}}{C_{8}^{3}}=\frac{5}{14}$,
$P(X = 1)=\frac{C_{2}^{1}C_{6}^{2}}{C_{8}^{3}}=\frac{15}{28}$,
$P(X = 2)=\frac{C_{2}^{2}C_{6}^{1}}{C_{8}^{3}}=\frac{3}{28}$.
所以 X 的分布列为
X 0 1 2
P $\frac{5}{14}$ $\frac{15}{28}$ $\frac{3}{28}$
所以$E(X)=0×\frac{5}{14}+1×\frac{15}{28}+2×\frac{3}{28}=\frac{3}{4}$.
(1)依题意,既有豆沙粽又有蜜枣粽的概率为$\frac{C_{2}^{1}C_{6}^{2}+C_{2}^{2}C_{6}^{1}}{C_{8}^{3}}=\frac{9}{14}$.
(2)X 的可能取值为 0,1,2.
$P(X = 0)=\frac{C_{2}^{0}C_{6}^{3}}{C_{8}^{3}}=\frac{5}{14}$,
$P(X = 1)=\frac{C_{2}^{1}C_{6}^{2}}{C_{8}^{3}}=\frac{15}{28}$,
$P(X = 2)=\frac{C_{2}^{2}C_{6}^{1}}{C_{8}^{3}}=\frac{3}{28}$.
所以 X 的分布列为
X 0 1 2
P $\frac{5}{14}$ $\frac{15}{28}$ $\frac{3}{28}$
所以$E(X)=0×\frac{5}{14}+1×\frac{15}{28}+2×\frac{3}{28}=\frac{3}{4}$.
答案:
解:
(1)依题意,既有豆沙粽又有蜜枣粽的概率为$\frac{C_{2}^{1}C_{6}^{2}+C_{2}^{2}C_{6}^{1}}{C_{8}^{3}}=\frac{9}{14}$.
(2)X 的可能取值为 0,1,2.
$P(X = 0)=\frac{C_{2}^{0}C_{6}^{3}}{C_{8}^{3}}=\frac{5}{14}$,
$P(X = 1)=\frac{C_{2}^{1}C_{6}^{2}}{C_{8}^{3}}=\frac{15}{28}$,
$P(X = 2)=\frac{C_{2}^{2}C_{6}^{1}}{C_{8}^{3}}=\frac{3}{28}$.
所以 X 的分布列为
X 0 1 2
P $\frac{5}{14}$ $\frac{15}{28}$ $\frac{3}{28}$
所以$E(X)=0×\frac{5}{14}+1×\frac{15}{28}+2×\frac{3}{28}=\frac{3}{4}$.
(1)依题意,既有豆沙粽又有蜜枣粽的概率为$\frac{C_{2}^{1}C_{6}^{2}+C_{2}^{2}C_{6}^{1}}{C_{8}^{3}}=\frac{9}{14}$.
(2)X 的可能取值为 0,1,2.
$P(X = 0)=\frac{C_{2}^{0}C_{6}^{3}}{C_{8}^{3}}=\frac{5}{14}$,
$P(X = 1)=\frac{C_{2}^{1}C_{6}^{2}}{C_{8}^{3}}=\frac{15}{28}$,
$P(X = 2)=\frac{C_{2}^{2}C_{6}^{1}}{C_{8}^{3}}=\frac{3}{28}$.
所以 X 的分布列为
X 0 1 2
P $\frac{5}{14}$ $\frac{15}{28}$ $\frac{3}{28}$
所以$E(X)=0×\frac{5}{14}+1×\frac{15}{28}+2×\frac{3}{28}=\frac{3}{4}$.
查看更多完整答案,请扫码查看


