2025年新坐标同步练习高中数学A版选择性必修第三册人教版青海专用
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新坐标同步练习高中数学A版选择性必修第三册人教版青海专用 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第38页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
典例 1
杨辉是我国南宋末年的一位杰出的数学家,其著作《详解九章算法》中画了一张表示二项式展开后的二项式系数构成的三角形数阵(如图所示),称做“开方作法本源”,现简称为“杨辉三角”,比西方的“帕斯卡三角形”早了 600 多年,若从第 0 行开始,用 $A_{(m,n)}$ 表示三角形数阵中的第 $m$ 行第 $n$ 个数,则 $A_{(101,3)}= $
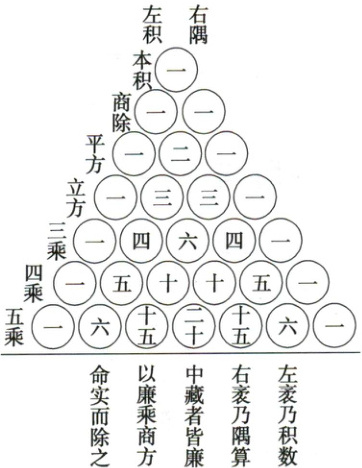
杨辉是我国南宋末年的一位杰出的数学家,其著作《详解九章算法》中画了一张表示二项式展开后的二项式系数构成的三角形数阵(如图所示),称做“开方作法本源”,现简称为“杨辉三角”,比西方的“帕斯卡三角形”早了 600 多年,若从第 0 行开始,用 $A_{(m,n)}$ 表示三角形数阵中的第 $m$ 行第 $n$ 个数,则 $A_{(101,3)}= $
5050
.(结果用数字作答)
答案:
5050
典例 2
在“杨辉三角”中,每一个数都是它“肩上”两个数的和,它开头几行如图所示. 那么,在“杨辉三角”中,第

在“杨辉三角”中,每一个数都是它“肩上”两个数的和,它开头几行如图所示. 那么,在“杨辉三角”中,第
62
行会出现三个相邻的数,其比为 $3:4:5$.
答案:
62
典例 3
杨辉三角(如图所示)是数学史上的一个伟大成就,杨辉三角中从第 2 行到第 2024 行,每行的第 3 个数字之和为(

A.$\mathrm{C}_{2024}^{3}$
B.$\mathrm{C}_{2025}^{3}$
C.$\mathrm{C}_{2024}^{3} - 1$
D.$\mathrm{C}_{2025}^{3} - 1$
杨辉三角(如图所示)是数学史上的一个伟大成就,杨辉三角中从第 2 行到第 2024 行,每行的第 3 个数字之和为(
B
)
A.$\mathrm{C}_{2024}^{3}$
B.$\mathrm{C}_{2025}^{3}$
C.$\mathrm{C}_{2024}^{3} - 1$
D.$\mathrm{C}_{2025}^{3} - 1$
答案:
B
1. “杨辉三角”是中国古代重要的数学成就,如图是由“杨辉三角”拓展而成的三角形数阵,记 $a_{n}$ 为图中所选数 $1,1,2,3,6,10,20,…$ 构成的数列 $\{ a_{n}\}$ 的第 $n$ 项,则 $a_{12}$ 的值为(
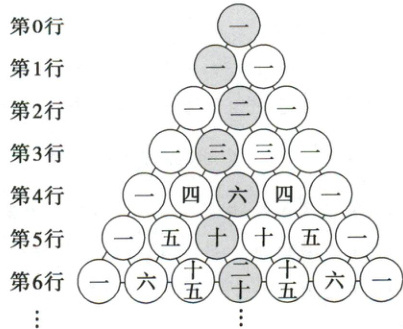
A.252
B.426
C.462
D.924
C
)
A.252
B.426
C.462
D.924
答案:
C
2. 将杨辉三角中的每一个数 $\mathrm{C}_{n}^{r}$ 都换成 $\frac{1}{(n + 1)\mathrm{C}_{n}^{r}}$,得到如图所示的分数三角形,称为莱布尼茨三角形. 莱布尼茨三角形具有很多优美的性质,如从第 0 行开始每一个数均等于其“脚下”两个数之和,如果 $n \geq 2$($n$ 为正整数),那么下面关于莱布尼茨三角形的结论中正确的是(
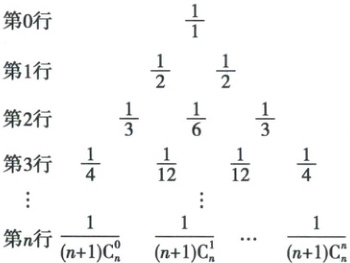
①当 $n$ 是偶数时,中间的一项取得最大值;当 $n$ 是奇数时,中间的两项相等,且同时取得最大值;②第 8 行第 2 个数是 $\frac{1}{72}$;③ $\frac{1}{(n + 1)\mathrm{C}_{n}^{r}} = \frac{1}{(n + 1)\mathrm{C}_{n}^{n - r}}(r \in \mathbf{N},0 \leq r \leq n)$.
A.①②
B.①③
C.②③
D.①②③
C
)
①当 $n$ 是偶数时,中间的一项取得最大值;当 $n$ 是奇数时,中间的两项相等,且同时取得最大值;②第 8 行第 2 个数是 $\frac{1}{72}$;③ $\frac{1}{(n + 1)\mathrm{C}_{n}^{r}} = \frac{1}{(n + 1)\mathrm{C}_{n}^{n - r}}(r \in \mathbf{N},0 \leq r \leq n)$.
A.①②
B.①③
C.②③
D.①②③
答案:
C
查看更多完整答案,请扫码查看


