《2025年新坐标同步练习高中数学A版选择性必修第三册人教版青海专用》

1. (教材P_2_7T_1_3改编)从5名男生和4名女生中选4人参加一项创新大赛,恰好3名男生与女生甲参加大赛的方法有(B)
A.6种
B.10种
C.15种
D.16种

答案： B

2. (多选)将甲、乙、丙、丁4名志愿者分别安排到A,B,C三个社区进行暑期社会实践活动,要求每个社区至少安排一名志愿者,则下列选项正确的是(BCD)
A.共有18种安排方法
B.若甲、乙被安排在同社区,则有6种安排方法
C.若A社区需要2名志愿者,则有12种安排方法
D.若甲被安排在A社区,则有12种安排方法

答案： BCD

3. (教材$P_2_6T_9$改编)某班准备利用班会的时间举行一场小型的文娱活动,准备表演3个歌唱类节目和2个语言类节目,现要排出一个节目单,若前2个节目中必须要有语言类节目,则不同的排法有84种.

答案： 84

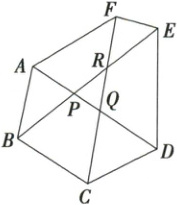
4. 如图,在六边形ABCDEF的6个顶点和其对角线AD,BE,CF的交点P,Q,R中,如果过其中的每3个点作一个圆,共可作多少个圆？

72

答案： 由题意得共九个点，任取三个点有$C_{9}^{3}=84$种选法，而三点共线的有$3C_{4}^{3}=12$（种），故能确定84-12=72个圆.

例1 从A,B,C等7人中选5人排成一排.
(1)若A必须在内,有多少种排法?
(2)若A,B,C都在内,且A,B必须相邻,C与A,B都不相邻,有多少种排法?
【解】（1）根据题意，若A必须在内，在其余6人中选出4人，再与A全排列，共有$C_{6}^{4}A_{5}^{5}=1800$种排法.
（2）根据题意，先在其他4人中选出2人，有$C_{4}^{2}=6$种选法，将A，B看成一个整体，与选出2人全排列，有$A_{3}^{3}A_{2}^{2}=12$种选法，排好后，有2个空位可用，在其中选出1个，安排C，有2种情况，所以共有$6×12×2=144$种不同的排法.

答案： 【解】（1）根据题意，若A必须在内，在其余6人中选出4人，再与A全排列，共有$C_{6}^{4}A_{5}^{5}=1800$种排法.
（2）根据题意，先在其他4人中选出2人，有$C_{4}^{2}=6$种选法，将A，B看成一个整体，与选出2人全排列，有$A_{3}^{3}A_{2}^{2}=12$种选法，排好后，有2个空位可用，在其中选出1个，安排C，有2种情况，所以共有$6×12×2=144$种不同的排法.