《2025年新坐标同步练习高中数学A版选择性必修第一册人教版青海专用》

3. 若圆 $C_1:(x - 2)^2 + y^2 = 1$ 与圆 $C_2:x^2 + y^2 + 4x + 6y + m = 0$ 有且仅有一条公切线,$m = $-23.

答案： 解析：由 C₂:x²+y²+4x + 6y + m = 0，可得(x + 2)²+(y + 3)²=13 - m，显然 13＞m，C₁(2,0)，C₂(-2,-3)，又圆 C₁ 与圆 C₂ 只有一条公切线，所以两圆相内切，将 C₂ 点坐标代入圆 C₁ 方程知(-2 - 2)²+(-3)²＞1，即 C₂ 在圆 C₁ 外部，所以圆 C₁ 内切于圆 C₂，则有|C₁C₂|=√((-2 - 2)²+(-3 - 0)²)=5=√(13 - m)-1，解得 m = -23.
答案：-23

4. 已知点 $P$ 是直线 $l_1:mx - y + m - 4 = 0$ 与直线 $l_2:x + my + 2m + 3 = 0$ 的交点,则点 $P$ 的轨迹方程为$(x + 2)^2+(y + 3)^2=2$;若点 $Q$ 是圆 $(x - 1)^2 + (y - 1)^2 = 1$ 上的动点,则 $|PQ|$ 的最大值为$6+\sqrt{2}$.

答案： 解析：因为直线 l₁:mx - y + m - 4=0，即 m(x + 1)-(y + 4)=0，令{x + 1=0,y + 4=0}，解得{x = -1,y = -4}，可知直线 l₁ 过定点 A(-1,-4)，同理可知，直线 l₂:x + my + 2m + 3=0 过定点 B(-3,-2)，又因为 m×1+(-1)×m = 0，可知 l₁⊥l₂，所以直线 l₁ 与直线 l₂ 的交点 P 的轨迹是以 AB 的中点 M(-2,-3)为圆心，r = 1/2|AB|=1/2×√((-1 + 3)²+(-4 + 2)²)=√2 为半径的圆，故点 P 的轨迹为圆(x + 2)²+(y + 3)²=2；(x - 1)²+(y - 1)²=1 的圆心为 C(1,1)，半径 R = 1，易知两圆外离，所以|PQ|的最大值是|MC|+r + R=√((-2 - 1)²+(-3 - 1)²)+√2+1=6+√2.
答案：(x + 2)²+(y + 3)²=2 6+√2

1. “陶辛水韵”于 1999 年被评为芜湖市新十景之一,每年入夏后,千亩水面莲叶接天,荷花映日,吸引远道游客纷至沓来,坐上游船穿过一座座圆拱桥,可以直达“香湖岛”赏荷.圆拱桥的水面跨度 20 米,拱高约 5 米.现有一船,水面以上高 3 米,欲通过圆拱桥,船宽最长约为(13米)

A.12 米
B.13 米
C.14 米
D.15 米

答案： 解析：选 B. 如图，拱形桥 ACB，以 AB 所在直线为 x 轴，以线段 AB 的垂直平分线为 y 轴，建立平面直角坐标系，则 A(-10,0)，B(10,0)，C(0,5)，圆心在 y 轴上，设为 E(0,b)，则有|AE|=|CE|，即√(100 + b²)=|5 - b|，整理可得 2b + 15=0，解得 b = -15/2，所以圆心为 E(0,-15/2)，半径为|CE|=|5 - b|=25/2，所以圆的方程为 x²+(y + 15/2)²=625/4. 设 D(x,3)，则有 x²+(3 + 15/2)²=625/4，解得 x = √46. 所以要使小船通过圆拱桥，船宽最长为 2√46. 因为 6.5＜√46＜7，所以 13＜2√46＜14，所以船宽最长约为 13 米.

2. 如图,第 25 届中国机器人及人工智能大赛总决赛中,主办方设计了一个矩形坐标场地 $ABCD$(包含地界和内部),$BC$ 长为 12 米,在 $AB$ 边上距离 $B$ 点 5 米的 $E$ 处放置一只机器犬,在距离 $B$ 点 2 米的 $F$ 处放置一个机器人,机器人行走的速度为 $v$,机器犬行走的速度为 $2v$,若机器犬和机器人在场地内沿着直线方向同时到达场地内某点 $P$(包含地界),则机器犬将被机器人捕获,点 $P$ 叫成功点.

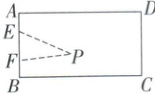
(1)求在这个矩形场地内成功点 $P$ 的轨迹方程;
(2)若 $N$ 为矩形场地 $BC$ 边上的一点,若机器犬在线段 $EN$ 上都能逃脱,问 $N$ 点应在何处?

答案： 解：
(1)如图 1，以 B 为原点，BC，BA 所在直线为 x，y 轴，建立平面直角坐标系，则 E(0,5)，F(0,2)，设成功点 P(x,y)，可得|PF|/v = |PE|/(2v)，即√(x²+(y - 2)²)/v = √(x²+(y - 5)²)/(2v)，化简得 x²+(y - 1)²=4. 因为点 P 在矩形场地内（包含地界），所以 0≤x≤2，故所求轨迹方程为 x²+(y - 1)²=4(0≤x≤2,0≤y≤3).
(2)当线段 EN 与
(1)中的圆相切时，sin∠BEP = 1/2，所以∠BEP = 30°，所以|BN|=5tan30°=5√3/3. 若机器犬在线段 EN 上都能逃脱，则 N 点横坐标的取值范围是(5√3/3,12].