《2025年新坐标同步练习高中数学A版选择性必修第一册人教版青海专用》

一 空间向量的夹角
思考 类比平面向量夹角的相关概念,探究空间向量的夹角概念。
空间向量的夹角：已知两个非零向量$\boldsymbol{a}$，$\boldsymbol{b}$，在空间任取一点$O$，作$\overrightarrow{OA}=\boldsymbol{a}$，$\overrightarrow{OB}=\boldsymbol{b}$，则$\angle AOB$叫做向量$\boldsymbol{a}$，$\boldsymbol{b}$的夹角，记作$\langle\boldsymbol{a},\boldsymbol{b}\rangle$。规定：$0\leqslant\langle\boldsymbol{a},\boldsymbol{b}\rangle\leqslant\pi$。当$\langle\boldsymbol{a},\boldsymbol{b}\rangle=0$时，$\boldsymbol{a}$与$\boldsymbol{b}$同向；当$\langle\boldsymbol{a},\boldsymbol{b}\rangle=\pi$时，$\boldsymbol{a}$与$\boldsymbol{b}$反向；当$\langle\boldsymbol{a},\boldsymbol{b}\rangle=\frac{\pi}{2}$时，称$\boldsymbol{a}$与$\boldsymbol{b}$互相垂直，记作$\boldsymbol{a}\perp\boldsymbol{b}$。

答案： 【解析】：空间向量的夹角：已知两个非零向量$\boldsymbol{a}$，$\boldsymbol{b}$，在空间任取一点$O$，作$\overrightarrow{OA}=\boldsymbol{a}$，$\overrightarrow{OB}=\boldsymbol{b}$，则$\angle AOB$叫做向量$\boldsymbol{a}$，$\boldsymbol{b}$的夹角，记作$\langle\boldsymbol{a},\boldsymbol{b}\rangle$。规定：$0\leqslant\langle\boldsymbol{a},\boldsymbol{b}\rangle\leqslant\pi$。当$\langle\boldsymbol{a},\boldsymbol{b}\rangle=0$时，$\boldsymbol{a}$与$\boldsymbol{b}$同向；当$\langle\boldsymbol{a},\boldsymbol{b}\rangle=\pi$时，$\boldsymbol{a}$与$\boldsymbol{b}$反向；当$\langle\boldsymbol{a},\boldsymbol{b}\rangle=\frac{\pi}{2}$时，称$\boldsymbol{a}$与$\boldsymbol{b}$互相垂直，记作$\boldsymbol{a}\perp\boldsymbol{b}$。
【答案】：见解析

答案： ①∠AOB ②0 ③π ④$\frac{π}{2}$

1. 判断正误,正确的打“√”,错误的打“×”。
(1) 空间向量 $\overrightarrow{AB}$ 与 $\overrightarrow{CD}$ 的夹角等于空间向量 $\overrightarrow{AB}$ 与 $\overrightarrow{DC}$ 的夹角。 (×)
(2) 对于空间非零向量 $\boldsymbol{a}$,$\boldsymbol{b}$,若 $\boldsymbol{a} // \boldsymbol{b}$,则 $\langle \boldsymbol{a}, \boldsymbol{b} \rangle = 0$。 (×)
(3) 对于空间非零向量 $\boldsymbol{a}$,$\boldsymbol{b}$,$\langle \boldsymbol{a}, \boldsymbol{b} \rangle$ 与 $\langle \boldsymbol{a}, -\boldsymbol{b} \rangle$ 相等。 (×)
(4) 在正四面体 $ABCD$ 中,$\overrightarrow{BC}$ 与 $\overrightarrow{CD}$ 的夹角等于 $60^{\circ}$。 (×)

答案： （1）× （2）× （3）× （4）×

2. 已知 $\boldsymbol{a}$,$\boldsymbol{b}$ 是空间非零向量,若 $|\boldsymbol{a}| = |\boldsymbol{b}| = |\boldsymbol{a} + \boldsymbol{b}|$,则 $\langle \boldsymbol{a}, \boldsymbol{b} \rangle = $$\frac{2π}{3}$。

答案： $\frac{2π}{3}$

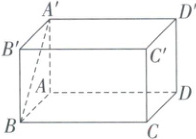
3. 如图,在长方体 $ABCD - A'B'C'D'$ 中,若 $AB = \sqrt{3}$,$AA' = 1$,则向量 $\overrightarrow{BA'}$ 与 $\overrightarrow{CC'}$ 的夹角为 $$$\frac{π}{3}$$$,$\overrightarrow{BA'}$ 与 $\overrightarrow{B'C'}$ 的夹角为 $$$\frac{π}{2}$$$。

答案： $\frac{π}{3}$ $\frac{π}{2}$

思考 1 回忆平面向量数量积的定义。
已知两个非零平面向量$\vec{a}$和$\vec{b}$，它们的夹角为$\theta(0\leq\theta\leq\pi)$，则数量$|\vec{a}||\vec{b}|\cos\theta$叫做$\vec{a}$与$\vec{b}$的数量积，记作$\vec{a}\cdot\vec{b}$，即$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta$；规定零向量与任一向量的数量积为0。

答案： 已知两个非零平面向量$\vec{a}$和$\vec{b}$，它们的夹角为$\theta(0\leq\theta\leq\pi)$，则数量$|\vec{a}||\vec{b}|\cos\theta$叫做$\vec{a}$与$\vec{b}$的数量积，记作$\vec{a}\cdot\vec{b}$，即$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta$；规定零向量与任一向量的数量积为0。

思考 2 类比平面向量数量积的性质与运算律,探究空间向量数量积的性质与运算律。
空间向量数量积的性质：
1. $\vec{a} \cdot \vec{a} = |\vec{a}|^2 \geq 0$，当且仅当$\vec{a} = \vec{0}$时取等号；
2. $\cos\theta = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}$（$\theta$为$\vec{a}$与$\vec{b}$的夹角，$\theta \in [0, \pi]$）；
3. 非零向量$\vec{a} \perp \vec{b} \Leftrightarrow \vec{a} \cdot \vec{b} = 0$；
4. $|\vec{a} \cdot \vec{b}| \leq |\vec{a}||\vec{b}|$，当且仅当$\vec{a}$与$\vec{b}$共线时取等号。
运算律：
1. 交换律：$\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}$；
2. 数乘结合律：$(\lambda \vec{a}) \cdot \vec{b} = \lambda (\vec{a} \cdot \vec{b}) = \vec{a} \cdot (\lambda \vec{b})$（$\lambda \in \mathbb{R}$）；
3. 分配律：$(\vec{a} + \vec{b}) \cdot \vec{c} = \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c}$。

答案： 【解析】：空间向量数量积的性质：
1. $\vec{a} \cdot \vec{a} = |\vec{a}|^2 \geq 0$，当且仅当$\vec{a} = \vec{0}$时取等号；
2. $\cos\theta = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}$（$\theta$为$\vec{a}$与$\vec{b}$的夹角，$\theta \in [0, \pi]$）；
3. 非零向量$\vec{a} \perp \vec{b} \Leftrightarrow \vec{a} \cdot \vec{b} = 0$；
4. $|\vec{a} \cdot \vec{b}| \leq |\vec{a}||\vec{b}|$，当且仅当$\vec{a}$与$\vec{b}$共线时取等号。
运算律：
1. 交换律：$\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}$；
2. 数乘结合律：$(\lambda \vec{a}) \cdot \vec{b} = \lambda (\vec{a} \cdot \vec{b}) = \vec{a} \cdot (\lambda \vec{b})$（$\lambda \in \mathbb{R}$）；
3. 分配律：$(\vec{a} + \vec{b}) \cdot \vec{c} = \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c}$。
【答案】：空间向量数量积的性质与运算律同平面向量，具体见解析。

1. 数量积的定义
已知两个非零向量 $\boldsymbol{a}$,$\boldsymbol{b}$,则 $|\boldsymbol{a}| |\boldsymbol{b}| \cos \langle \boldsymbol{a}, \boldsymbol{b} \rangle$ 叫做 $\boldsymbol{a}$,$\boldsymbol{b}$ 的数量积,记作 $\underline{①}$。即 $\boldsymbol{a} \cdot \boldsymbol{b} = \underline{②}$。
①a·b ②|a||b|cos〈a，b〉

答案： ①a·b ②|a||b|cos〈a，b〉