《2025年新坐标同步练习高中数学A版选择性必修第一册人教版青海专用》

直线 $ Ax + By + C = 0 $ 与圆 $ (x - a)^2 + (y - b)^2 = r^2 $ 的位置关系的判断

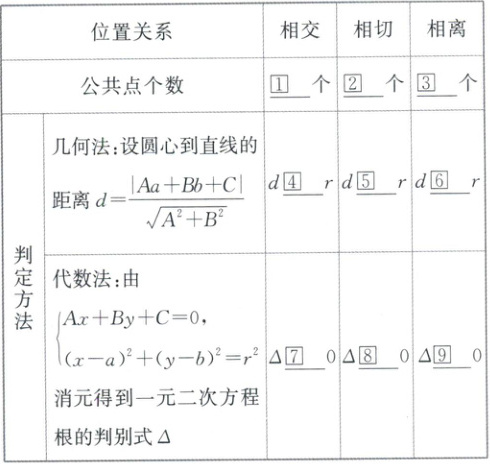
答案： ①2 ②1 ③0 ④＜ ⑤= ⑥＞ ⑦＞ ⑧= ⑨＜

1. 已知直线 $ l: x + y + 2 = 0 $ 和圆 $ C: x^2 + y^2 - 2x - 4y - 3 = 0 $,则直线 $ l $ 与圆 $ C $ 的位置关系是 (C)
A.相交
B.相切
C.相离
D.相交或相切

答案： C

2. “直线 $ ax + by - 1 = 0 $ 与圆 $ x^2 + y^2 = 1 $ 相交”是“$ a^2 + b^2 \geq 1 $”的 (A)
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件

答案： A

3. 已知圆 $ C $ 经过直线 $ y = x - 1 $ 与圆 $ x^2 + y^2 = 1 $ 的公共点和点 $ (1,1) $,则圆 $ C $ 的一般方程为 x²+y²+x-y-2=0.

答案： x²+y²+x-y-2=0

4. 若直线 $ l: x + y - m = 0 $ 与曲线 $ C: y = \sqrt{9 - x^2} $ 只有一个公共点,则实数 $ m $ 的取值范围是 [-3,3)∪{3√2}.

答案： [-3,3)∪{3√2}

[例1] (对接教材例1) 已知圆 $ C: x^2 + y^2 - 4x - 4y + 4 = 0 $,直线 $ l: x + my - 1 - m = 0 $.
(1) 求证：无论实数 $ m $ 取何值,直线 $ l $ 与圆 $ C $ 都相交；
(2) 当 $ m = 1 $ 时,求直线 $ l $ 被圆 $ C $ 截得的弦长.
(1)证明:因为直线方程可化为x-1+m(y-1)=0,由{x-1=0, y-1=0可得{x=1, y=1,所以直线恒过定点(1,1),把(1,1)代入圆C方程得1²+1²-4-4+4=-2＜0,所以定点(1,1)始终在圆C内,所以无论实数m取何值，直线l与圆C都相交.
(2)方法一:圆C:x²+y²-4x-4y+4=0化为(x-2)²+(y-2)²=4,圆心C(2,2),半径r=2.
当m=1时,直线l:x+y-2=0.
圆心C到直线l的距离d=|2+2-2|/√(1+1)=√2.
所以直线l被圆C截得的弦长为2√(r²-d²)=2×√(4-2)=2√2.
方法二:当m=1时,直线l:x+y-2=0.
联立{x²+y²-4x-4y+4=0, x+y-2=0,整理得x²-2x=0,得{x=0, y=2或{x=2, y=0,设直线l与圆C相交于A(0,2),B(2,0),所以弦长|AB|=√[(0-2)²+(2-0)²]=2√2.
方法三:在方法二中,也可以不求交点坐标,设A(x₁,y₁),B(x₂,y₂),由x²-2x=0可得x₁+x₂=2,x₁x₂=0,由弦长公式|AB|=√(1+k²)·√[(x₁+x₂)²-4x₁x₂]=√[1+(-1)²]×√(2²-4×0)=2√2.

答案：
(1)证明:因为直线方程可化为x-1+m(y-1)=0,由{x-1=0, y-1=0可得{x=1, y=1,所以直线恒过定点(1,1),把(1,1)代入圆C方程得1²+1²-4-4+4=-2＜0,所以定点(1,1)始终在圆C内,所以无论实数m取何值，直线l与圆C都相交.
(2)方法一:圆C:x²+y²-4x-4y+4=0化为(x-2)²+(y-2)²=4,圆心C(2,2),半径r=2.
当m=1时,直线l:x+y-2=0.
圆心C到直线l的距离d=|2+2-2|/√(1+1)=√2.
所以直线l被圆C截得的弦长为2√(r²-d²)=2×√(4-2)=2√2.
方法二:当m=1时,直线l:x+y-2=0.
联立{x²+y²-4x-4y+4=0, x+y-2=0,整理得x²-2x=0,得{x=0, y=2或{x=2, y=0,设直线l与圆C相交于A(0,2),B(2,0),所以弦长|AB|=√[(0-2)²+(2-0)²]=2√2.
方法三:在方法二中,也可以不求交点坐标,设A(x₁,y₁),B(x₂,y₂),由x²-2x=0可得x₁+x₂=2,x₁x₂=0,由弦长公式|AB|=√(1+k²)·√[(x₁+x₂)²-4x₁x₂]=√[1+(-1)²]×√(2²-4×0)=2√2.