2025年新坐标同步练习高中物理选择性必修第三册人教版青海专用
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新坐标同步练习高中物理选择性必修第三册人教版青海专用 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第30页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. (封闭气体压强的计算) 如图所示,两端开口的弯折的玻璃管竖直放置,三段竖直管内各有一段水银柱,两段空气封闭在三段水银柱之间。若左、右两管内水银柱长度分别为 $ h_1 $、$ h_2 $,且水银柱均静止,则中间管内水银柱的长度为(
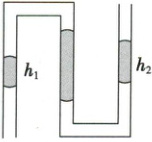
A.$ h_1 - h_2 $
B.$ h_1 + h_2 $
C.$ \frac{h_1 - h_2}{2} $
D.$ \frac{h_1 + h_2}{2} $
B
)
A.$ h_1 - h_2 $
B.$ h_1 + h_2 $
C.$ \frac{h_1 - h_2}{2} $
D.$ \frac{h_1 + h_2}{2} $
答案:
B
2. (玻意耳定律) (2024·广东东莞阶段练) 粗细均匀且足够长的玻璃管一端封闭,管内有一段长度 $ h = 15 \, cm $ 的水银柱。当玻璃管开口向上竖直放置时,管内被水银柱封闭的空气柱长度 $ L_1 = 20 \, cm $,如图甲所示,现将玻璃管缓慢地转到水平位置时,空气柱长度变为 $ L_2 $,如图乙所示。设整个过程中玻璃管内气体温度保持不变,大气压强 $ p_0 = 75 \, cmHg $。求:
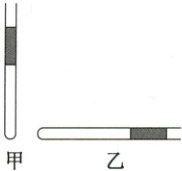
(1) 玻璃管开口向上竖直放置时管内被水银柱封闭的空气柱的压强 $ p_1 $ 和玻璃管水平位置放置时被水银柱封闭的空气柱的压强 $ p_2 $(以 $ cmHg $ 为单位);
(2) 图乙中封闭空气柱的长度 $ L_2 $。
(1)
(2)

(1) 玻璃管开口向上竖直放置时管内被水银柱封闭的空气柱的压强 $ p_1 $ 和玻璃管水平位置放置时被水银柱封闭的空气柱的压强 $ p_2 $(以 $ cmHg $ 为单位);
(2) 图乙中封闭空气柱的长度 $ L_2 $。
(1)
90cmHg
75cmHg
(2)
24cm
答案:
(1)90cmHg 75cmHg
(2)24cm
(1)90cmHg 75cmHg
(2)24cm
3. (玻意耳定律) (2024·广东深圳一模) 遇到突发洪水时,可以借助塑料盆进行自救,简化模型如下,塑料盆近似看成底面积为 $ S $ 的圆柱形容器,把塑料盆口向下竖直轻放在静止水面上,用力竖直向下缓慢压盆底,当压力为 $ F $ 时恰好使盆底与液面相平,忽略塑料盆的厚度及盆所受的重力,已知大气压强为 $ p_0 $,重力加速度为 $ g $,水的密度为 $ \rho $,求:
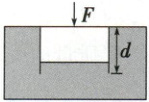
(1) 此时盆内空气的压强 $ p $;
(2) 此时塑料盆口的深度 $ d $。

(1) 此时盆内空气的压强 $ p $;
(2) 此时塑料盆口的深度 $ d $。
(1)$p_{0}+\frac{F}{S}$ (2)$(1+\frac{F}{p_{0}S})\cdot\frac{F}{\rho gS}$
答案:
(1)$p_{0}+\frac{F}{S}$
(2)$(1+\frac{F}{p_{0}S})\cdot\frac{F}{\rho gS}$
(1)$p_{0}+\frac{F}{S}$
(2)$(1+\frac{F}{p_{0}S})\cdot\frac{F}{\rho gS}$
查看更多完整答案,请扫码查看


