《2025年同步练习册配套检测卷六年级数学上册鲁教版五四制》

20. (6分)有理数$a$,$b$,$c$表示的点在数轴上的位置如图所示.

(1) 用“$＞$”或“$＜$”填空:$b$$＜$$-1$;$a$$＜$$1$;$c$$＞$$b$.
(2) 化简:$|b + 1|+|a - 1|-|c - b|$.
$-a - c$

答案：
(1) $b＜ -1$；$a ＜ 1$；$c ＞ b$。
(2) 由数轴可知$b＜ -1$，$ -1＜a＜0$，$c＞1$，所以$b + 1＜0$，$a - 1＜0$，$c - b＞0$。
则$\vert b + 1\vert+\vert a - 1\vert-\vert c - b\vert=-(b + 1)-(a - 1)-(c - b)=-b - 1 - a + 1 - c + b=-a - c$。

21. (8分)某校学生会为了解该校2860名学生最喜欢的球类活动的情况,采取抽样调查的办法,从足球、乒乓球、篮球、排球四个方面调查了若干名学生的兴趣爱好,并将调查的结果绘制成两幅不完整的统计图(如图1,2,要求每名同学只能选择一种自己喜欢的球类活动).请你根据图中提供的信息,解答下列问题:


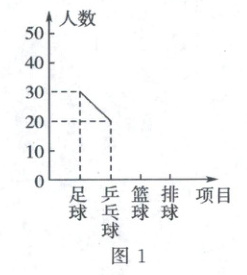
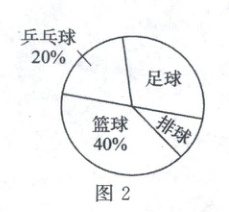
(1) 一共调查了100名学生.
(2) 在扇形统计图中“排球”对应的扇形圆心角是36$^{\circ}$.
(3) 补全折线统计图.
(4) 估计该校喜欢排球的学生的人数.
（3）喜欢排球的人数为10人，在折线统计图中对应位置标出10即可；（4）286人

答案： （1）由图1，图2可知：
喜欢乒乓球的人数为$20$人，占总人数的$20\%$，
所以总人数为：$20÷20\%=100$（名）。
（2）喜欢篮球的人数为$40$人，
喜欢篮球的人数占总人数的：$40÷100×100\%=40\%$，
喜欢排球的人数占总人数的：
$1-20\%-40\%-喜欢足球人数占比$，
喜欢足球的人数为$30$人，
喜欢足球的人数占总人数的：$30÷100×100\%=30\%$，
所以喜欢排球的人数占总人数的：
$1-20\%-40\%-30\%=10\%$，
在扇形统计图中“排球”对应的扇形圆心角是：
$360^{\circ}×10\%=36^{\circ}×1=36^{\circ}$。
（3）喜欢排球的人数为：
$100×10\%=10$（人），
在折线统计图中，排球对应的人数为$10$，在图上表示出即可。
（4）$2860×10\%=286$（人），
所以，估计该校喜欢排球的学生的人数为$286$人。