《2025年同步练习册配套检测卷六年级数学上册鲁教版五四制》

23. (10 分)如图是由非负偶数排成的数阵：

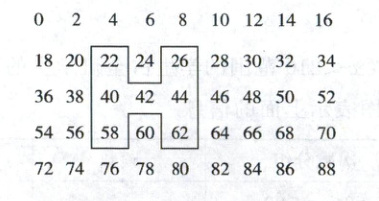
(1)写出图中 H 形框中七个数的和与中间数的关系；
(2)在数阵中任意做一个这样的 H 形框,(1)中的关系是否仍成立？并写出理由；
(3)用这样的 H 形框能框出和为 2023 的七个数吗？如果能,求出这七个数中间的数；如果不能,请写出理由.

答案：
(1) 七个数的和是中间数的7倍。
(2) 成立。设中间数为$x$，数阵中同一列上下相邻数相差18，左右相邻数相差2。则H形框中七个数分别为$(x-20)$，$(x-18)$，$(x-16)$，$x$，$(x+16)$，$(x+18)$，$(x+20)$。其和为$(x-20)+(x-18)+(x-16)+x+(x+16)+(x+18)+(x+20)=7x$，故和是中间数的7倍。
(3) 不能。因为$2023÷7=289$，289为奇数，而数阵中的数均为非负偶数，中间数不可能为奇数，所以不能框出。