第46页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
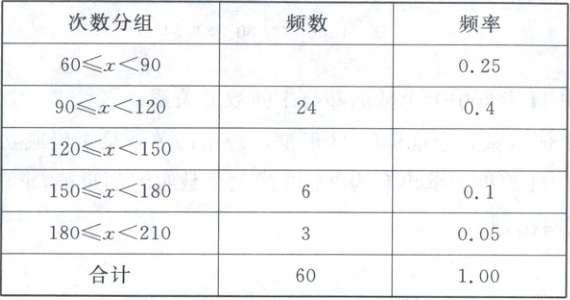
21. (8 分)体育委员统计了全班同学 60 秒跳绳的次数,并列出不完全的频数分布表.
(1)补全表中信息.
(2)跳绳次数在$120\leqslant x\lt210$范围的学生占全班学生的百分比是多少?
(3)画出适当的统计图表示上面的信息.
(1)补全表中信息.
(2)跳绳次数在$120\leqslant x\lt210$范围的学生占全班学生的百分比是多少?
(3)画出适当的统计图表示上面的信息.

答案:
(1)
总人数为$60$人,$60\leqslant x\lt90$的频数为$60×0.25 = 15$;
$120\leqslant x\lt150$的频数为$60-(15 + 24+6 + 3)=12$,频率为$12÷60 = 0.2$。
填表如下:
|次数分组|频数|频率|
| ---- | ---- | ---- |
|$60\leqslant x\lt90$| $15$| $0.25$|
|$90\leqslant x\lt120$| $24$| $0.4$|
|$120\leqslant x\lt150$| $12$| $0.2$|
|$150\leqslant x\lt180$| $6$| $0.1$|
|$180\leqslant x\lt210$| $3$| $0.05$|
|合计| $60$| $1.00$|
(2)
跳绳次数在$120\leqslant x\lt210$范围的学生频数为$12 + 6+3=21$,占全班学生的百分比为$\frac{21}{60}×100\% = 35\%$。
(3)
绘制频数分布直方图:
横轴表示次数分组,纵轴表示频数,根据各次数分组的频数绘制相应的矩形,矩形高度对应频数。
(1)
总人数为$60$人,$60\leqslant x\lt90$的频数为$60×0.25 = 15$;
$120\leqslant x\lt150$的频数为$60-(15 + 24+6 + 3)=12$,频率为$12÷60 = 0.2$。
填表如下:
|次数分组|频数|频率|
| ---- | ---- | ---- |
|$60\leqslant x\lt90$| $15$| $0.25$|
|$90\leqslant x\lt120$| $24$| $0.4$|
|$120\leqslant x\lt150$| $12$| $0.2$|
|$150\leqslant x\lt180$| $6$| $0.1$|
|$180\leqslant x\lt210$| $3$| $0.05$|
|合计| $60$| $1.00$|
(2)
跳绳次数在$120\leqslant x\lt210$范围的学生频数为$12 + 6+3=21$,占全班学生的百分比为$\frac{21}{60}×100\% = 35\%$。
(3)
绘制频数分布直方图:
横轴表示次数分组,纵轴表示频数,根据各次数分组的频数绘制相应的矩形,矩形高度对应频数。
22. (10 分)甲乙两队进行拔河比赛,标志物先向甲队方向移动$0.5m$,后向乙队方向移动了$0.8m$;相持一会后又向乙队方向移动$0.5m$,随后向甲队方向移动了$1.5m$;在一片欢呼声中,标志物再向甲队方向移动$1.2m$.若规定只要标志物向某队方向移动$2m$,则该队即可获胜,那么现在甲队获胜了吗?用计算说明理由.
答案:
设标志物向甲队方向移动的米数记为正,向乙队方向移动的米数记为负。
将每次移动的距离进行加减计算:
$+ 0.5 - 0.8 - 0.5 + 1.5 + 1.2$
$= 0.5 + (- 0.8) + (- 0.5) + 1.5 + 1.2$
$= (0.5 + 1.5 + 1.2) + (- 0.8 - 0.5)$
$= 3.2 - 1.3$
$= 1.9(m)$
因为$1.9m\lt 2m$。
所以甲队没有获胜。
将每次移动的距离进行加减计算:
$+ 0.5 - 0.8 - 0.5 + 1.5 + 1.2$
$= 0.5 + (- 0.8) + (- 0.5) + 1.5 + 1.2$
$= (0.5 + 1.5 + 1.2) + (- 0.8 - 0.5)$
$= 3.2 - 1.3$
$= 1.9(m)$
因为$1.9m\lt 2m$。
所以甲队没有获胜。
查看更多完整答案,请扫码查看


