2025年新坐标同步练习高中物理必修第一册人教版青海专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新坐标同步练习高中物理必修第一册人教版青海专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
[学习笔记]
角度2 平均速度和平均速率
例5
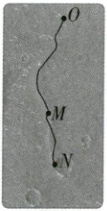
A.从$O处行驶到N处的路程为697$米
B.从$O处行驶到N处的位移大小为889$米
C.从$O处行驶到M处的平均速率约为20$米/天
D.从$M处行驶到N处的平均速度大小约为10$米/天
角度2 平均速度和平均速率
例5

D
A.从$O处行驶到N处的路程为697$米
B.从$O处行驶到N处的位移大小为889$米
C.从$O处行驶到M处的平均速率约为20$米/天
D.从$M处行驶到N处的平均速度大小约为10$米/天
答案:
D
例6
(多选)$A$、$B$两物体沿同一直线运动,运动过程中的$x - t$图像如图所示,下列说法正确的是(
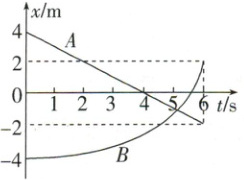
A.$4s时A$物体运动方向没有发生改变
B.前$6s内B$物体的速度逐渐减小
C.前$5s$内两物体的平均速度相等
D.前$6s$内某时刻两物体的速度大小相等
(多选)$A$、$B$两物体沿同一直线运动,运动过程中的$x - t$图像如图所示,下列说法正确的是(
AD
)
A.$4s时A$物体运动方向没有发生改变
B.前$6s内B$物体的速度逐渐减小
C.前$5s$内两物体的平均速度相等
D.前$6s$内某时刻两物体的速度大小相等
答案:
AD
【教材经典 P34 第 2 题】如图所示的是某物体做直线运动的$x - t$图像,请说明$x - t$图像中每段运动过程的速度大小和方向,并作出$v - t$图像,描述相应过程。
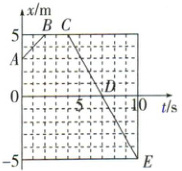
1. 首先求$AB$段:
公式:根据速度公式$v=\frac{\Delta x}{\Delta t}$,$x - t$图像的斜率表示速度。
计算:$A(0,1)$,$B(2,5)$,$\Delta x = x_{B}-x_{A}=5 - 1=4m$,$\Delta t=t_{B}-t_{A}=2 - 0 = 2s$。
结果:$v_{AB}=\frac{\Delta x}{\Delta t}=\frac{5 - 1}{2}=2m/s$,方向沿$x$轴正方向。
2. 然后求$BC$段:
公式:$v=\frac{\Delta x}{\Delta t}$。
计算:$B(2,5)$,$C(5,5)$,$\Delta x=x_{C}-x_{B}=5 - 5 = 0$,$\Delta t=t_{C}-t_{B}=5 - 2 = 3s$。
结果:$v_{BC}=\frac{\Delta x}{\Delta t}=0$,物体静止。
3. 接着求$CD$段:
公式:$v=\frac{\Delta x}{\Delta t}$。
计算:$C(5,5)$,$D(7,0)$,$\Delta x=x_{D}-x_{C}=0 - 5=-5m$,$\Delta t=t_{D}-t_{C}=7 - 5 = 2s$。
结果:$v_{CD}=\frac{\Delta x}{\Delta t}=\frac{0 - 5}{2}=-2.5m/s$,方向沿$x$轴负方向。
4. 最后求$DE$段:
公式:$v=\frac{\Delta x}{\Delta t}$。
计算:$D(7,0)$,$E(10,-5)$,$\Delta x=x_{E}-x_{D}=-5 - 0=-5m$,$\Delta t=t_{E}-t_{D}=10 - 7 = 3s$。
结果:$v_{DE}=\frac{\Delta x}{\Delta t}=\frac{-5-0}{3}=-\frac{5}{3}m/s\approx - 1.67m/s$,方向沿$x$轴负方向。
5. 绘制$v - t$图像:
$0 - 2s$,$v = 2m/s$(水平直线,$v\gt0$);
$2 - 5s$,$v = 0$($v = 0$的直线);
$5 - 7s$,$v=-2.5m/s$(水平直线,$v\lt0$);
$7 - 10s$,$v =-\frac{5}{3}m/s$(水平直线,$v\lt0$)。
描述:物体先以$2m/s$的速度沿$x$轴正方向做匀速直线运动,接着静止$3s$,然后以$2.5m/s$的速度沿$x$轴负方向做匀速直线运动,最后以$\frac{5}{3}m/s$的速度沿$x$轴负方向做匀速直线运动。

1. 首先求$AB$段:
公式:根据速度公式$v=\frac{\Delta x}{\Delta t}$,$x - t$图像的斜率表示速度。
计算:$A(0,1)$,$B(2,5)$,$\Delta x = x_{B}-x_{A}=5 - 1=4m$,$\Delta t=t_{B}-t_{A}=2 - 0 = 2s$。
结果:$v_{AB}=\frac{\Delta x}{\Delta t}=\frac{5 - 1}{2}=2m/s$,方向沿$x$轴正方向。
2. 然后求$BC$段:
公式:$v=\frac{\Delta x}{\Delta t}$。
计算:$B(2,5)$,$C(5,5)$,$\Delta x=x_{C}-x_{B}=5 - 5 = 0$,$\Delta t=t_{C}-t_{B}=5 - 2 = 3s$。
结果:$v_{BC}=\frac{\Delta x}{\Delta t}=0$,物体静止。
3. 接着求$CD$段:
公式:$v=\frac{\Delta x}{\Delta t}$。
计算:$C(5,5)$,$D(7,0)$,$\Delta x=x_{D}-x_{C}=0 - 5=-5m$,$\Delta t=t_{D}-t_{C}=7 - 5 = 2s$。
结果:$v_{CD}=\frac{\Delta x}{\Delta t}=\frac{0 - 5}{2}=-2.5m/s$,方向沿$x$轴负方向。
4. 最后求$DE$段:
公式:$v=\frac{\Delta x}{\Delta t}$。
计算:$D(7,0)$,$E(10,-5)$,$\Delta x=x_{E}-x_{D}=-5 - 0=-5m$,$\Delta t=t_{E}-t_{D}=10 - 7 = 3s$。
结果:$v_{DE}=\frac{\Delta x}{\Delta t}=\frac{-5-0}{3}=-\frac{5}{3}m/s\approx - 1.67m/s$,方向沿$x$轴负方向。
5. 绘制$v - t$图像:
$0 - 2s$,$v = 2m/s$(水平直线,$v\gt0$);
$2 - 5s$,$v = 0$($v = 0$的直线);
$5 - 7s$,$v=-2.5m/s$(水平直线,$v\lt0$);
$7 - 10s$,$v =-\frac{5}{3}m/s$(水平直线,$v\lt0$)。
描述:物体先以$2m/s$的速度沿$x$轴正方向做匀速直线运动,接着静止$3s$,然后以$2.5m/s$的速度沿$x$轴负方向做匀速直线运动,最后以$\frac{5}{3}m/s$的速度沿$x$轴负方向做匀速直线运动。
答案:
1. 首先求$AB$段:
公式:根据速度公式$v=\frac{\Delta x}{\Delta t}$,$x - t$图像的斜率表示速度。
计算:$A(0,1)$,$B(2,5)$,$\Delta x = x_{B}-x_{A}=5 - 1=4m$,$\Delta t=t_{B}-t_{A}=2 - 0 = 2s$。
结果:$v_{AB}=\frac{\Delta x}{\Delta t}=\frac{5 - 1}{2}=2m/s$,方向沿$x$轴正方向。
2. 然后求$BC$段:
公式:$v=\frac{\Delta x}{\Delta t}$。
计算:$B(2,5)$,$C(5,5)$,$\Delta x=x_{C}-x_{B}=5 - 5 = 0$,$\Delta t=t_{C}-t_{B}=5 - 2 = 3s$。
结果:$v_{BC}=\frac{\Delta x}{\Delta t}=0$,物体静止。
3. 接着求$CD$段:
公式:$v=\frac{\Delta x}{\Delta t}$。
计算:$C(5,5)$,$D(7,0)$,$\Delta x=x_{D}-x_{C}=0 - 5=-5m$,$\Delta t=t_{D}-t_{C}=7 - 5 = 2s$。
结果:$v_{CD}=\frac{\Delta x}{\Delta t}=\frac{0 - 5}{2}=-2.5m/s$,方向沿$x$轴负方向。
4. 最后求$DE$段:
公式:$v=\frac{\Delta x}{\Delta t}$。
计算:$D(7,0)$,$E(10,-5)$,$\Delta x=x_{E}-x_{D}=-5 - 0=-5m$,$\Delta t=t_{E}-t_{D}=10 - 7 = 3s$。
结果:$v_{DE}=\frac{\Delta x}{\Delta t}=\frac{-5-0}{3}=-\frac{5}{3}m/s\approx - 1.67m/s$,方向沿$x$轴负方向。
5. 绘制$v - t$图像:
$0 - 2s$,$v = 2m/s$(水平直线,$v\gt0$);
$2 - 5s$,$v = 0$($v = 0$的直线);
$5 - 7s$,$v=-2.5m/s$(水平直线,$v\lt0$);
$7 - 10s$,$v =-\frac{5}{3}m/s$(水平直线,$v\lt0$)。
描述:物体先以$2m/s$的速度沿$x$轴正方向做匀速直线运动,接着静止$3s$,然后以$2.5m/s$的速度沿$x$轴负方向做匀速直线运动,最后以$\frac{5}{3}m/s$的速度沿$x$轴负方向做匀速直线运动。
公式:根据速度公式$v=\frac{\Delta x}{\Delta t}$,$x - t$图像的斜率表示速度。
计算:$A(0,1)$,$B(2,5)$,$\Delta x = x_{B}-x_{A}=5 - 1=4m$,$\Delta t=t_{B}-t_{A}=2 - 0 = 2s$。
结果:$v_{AB}=\frac{\Delta x}{\Delta t}=\frac{5 - 1}{2}=2m/s$,方向沿$x$轴正方向。
2. 然后求$BC$段:
公式:$v=\frac{\Delta x}{\Delta t}$。
计算:$B(2,5)$,$C(5,5)$,$\Delta x=x_{C}-x_{B}=5 - 5 = 0$,$\Delta t=t_{C}-t_{B}=5 - 2 = 3s$。
结果:$v_{BC}=\frac{\Delta x}{\Delta t}=0$,物体静止。
3. 接着求$CD$段:
公式:$v=\frac{\Delta x}{\Delta t}$。
计算:$C(5,5)$,$D(7,0)$,$\Delta x=x_{D}-x_{C}=0 - 5=-5m$,$\Delta t=t_{D}-t_{C}=7 - 5 = 2s$。
结果:$v_{CD}=\frac{\Delta x}{\Delta t}=\frac{0 - 5}{2}=-2.5m/s$,方向沿$x$轴负方向。
4. 最后求$DE$段:
公式:$v=\frac{\Delta x}{\Delta t}$。
计算:$D(7,0)$,$E(10,-5)$,$\Delta x=x_{E}-x_{D}=-5 - 0=-5m$,$\Delta t=t_{E}-t_{D}=10 - 7 = 3s$。
结果:$v_{DE}=\frac{\Delta x}{\Delta t}=\frac{-5-0}{3}=-\frac{5}{3}m/s\approx - 1.67m/s$,方向沿$x$轴负方向。
5. 绘制$v - t$图像:
$0 - 2s$,$v = 2m/s$(水平直线,$v\gt0$);
$2 - 5s$,$v = 0$($v = 0$的直线);
$5 - 7s$,$v=-2.5m/s$(水平直线,$v\lt0$);
$7 - 10s$,$v =-\frac{5}{3}m/s$(水平直线,$v\lt0$)。
描述:物体先以$2m/s$的速度沿$x$轴正方向做匀速直线运动,接着静止$3s$,然后以$2.5m/s$的速度沿$x$轴负方向做匀速直线运动,最后以$\frac{5}{3}m/s$的速度沿$x$轴负方向做匀速直线运动。
例7
(多选)做直线运动的物体,其$v - t$图像如图所示,下列判断正确的是( )
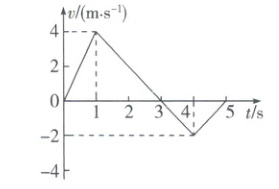
A.物体在$1s$末改变运动方向
B.物体在前$3s$内运动方向不变
C.物体在$3s$末运动方向改变
D.物体在$2s末时的速度大小为2m/s$
(多选)做直线运动的物体,其$v - t$图像如图所示,下列判断正确的是( )

A.物体在$1s$末改变运动方向
B.物体在前$3s$内运动方向不变
C.物体在$3s$末运动方向改变
D.物体在$2s末时的速度大小为2m/s$
答案:
BCD
查看更多完整答案,请扫码查看


