《2025年基础训练大象出版社九年级数学全一册人教版》

14. (★★)下列四边形既是轴对称图形,又是中心对称图形的是【C】
A.对角线互相垂直的四边形
B.对角线互相平分的四边形
C.对角线互相垂直且平分的四边形
D.对角线互相垂直且相等的四边形

答案： C

15. (★★)如图 23.2-22,图①、图②均为 7×6 的网格,点 A,B,C 在格点(小正方形的顶点)上.
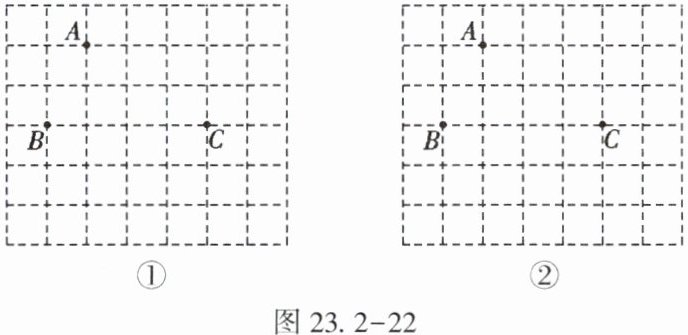
(1)在图①中确定格点 D,并画出一个以 A,B,C,D 为顶点的四边形,使其为轴对称图形；
(2)在图②中确定格点 E,并画出一个以 A,B,C,E 为顶点的四边形,使其为中心对称图形.

答案：
(1) 如图①，取格点D（A关于线段BC垂直平分线的对称点），连接A、B、C、D，四边形ABCD即为所求轴对称图形。
(2) 如图②，取格点E（使得AE平行且等于BC），连接A、B、C、E，四边形ABCE即为所求中心对称图形。
（注：此处需根据实际图形确定D、E的具体格点位置，上述描述为基于常见网格点位置的规范作答。）

16. (★★)如图 23.2-23,在△ABC 中,点 O 是 AB 的中点.
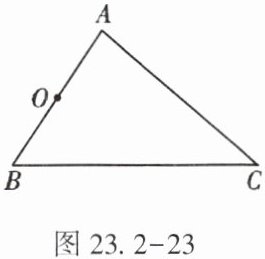
(1)请你作出以点 O 为旋转中心,将△ABC 旋转 180°后的△A'B'C'.
(2)△ABC 与△A'B'C'拼成的四边形是什么四边形？请说明理由.
(3)第(2)问的四边形是中心对称图形吗？

答案：
(1)作图步骤：①连接CO并延长至C'，使OC'=OC；②点A绕O旋转180°得A'=B，点B绕O旋转180°得B'=A；③连接A'B'、B'C'、A'C'，△A'B'C'即为所求。
(2)平行四边形。理由：由旋转性质知OC=OC'，OA=OA'=OB，OB=OB'=OA，故四边形ACBC'的对角线AB与CC'互相平分，所以是平行四边形。
(3)是。

17. (★)(2022·山西)2022 年 4 月 16 日,神舟十三号载人飞船圆满完成全部既定任务,顺利返回地球家园.6 个月的飞天之旅展现了中国航天科技的新高度.图 23.2-24 所示的航天图标,其文字上方的图案是中心对称图形的是【B】

答案： B

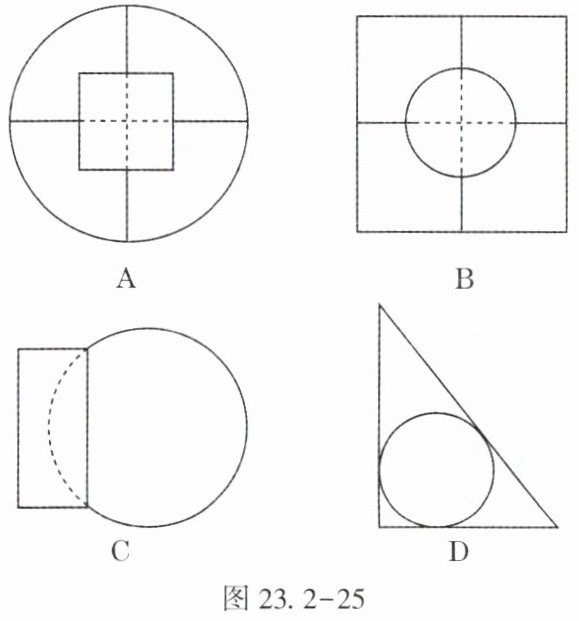
18. (★)(2025·福建)中国古算诗词歌赋较多.古算诗词题,是反映数学数量关系的内在联系及规律的一种文学浪漫形式.图 23.2-25 分别是古算诗词题“圆中方形”“方形圆径”“圆材藏壁”“勾股容圆”所描绘的图形,其中既不是轴对称图形也不是中心对称图形的是【D】

答案： D