《2025年基础训练大象出版社八年级数学上册人教版》

23. (11分)定义:在一个三角形中,如果有一个角的度数是另一个角的度数的$\frac{1}{2}$},我们称这两个角互为“友爱角”,这个三角形叫作“友爱三角形”.例如:在△ABC中,如果∠A= 80°,∠B= 40°,那么∠A与∠B互为“友爱角”,△ABC是“友爱三角形”.
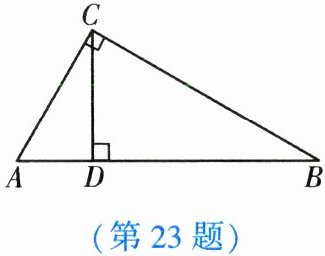
如图,△ABC是“友爱三角形”,且∠A与∠B互为“友爱角”(∠A＞∠B),∠ACB= 90°.
(1)求∠A,∠B的度数.
(2)若CD是△ABC中边AB上的高,则△ACD,△BCD都是“友爱三角形”吗? 为什么?

答案：
(1)
∵　　∠A与∠B互为“友爱角”,且∠A＞∠B,
∴　　∠B= $\frac{1}{2}$∠A.
∴　　∠A=2∠B.
在△ABC中,∠ACB=90°,
∴　　∠A+∠B=90°.
∴　　2∠B+∠B=90°.
∴　　∠B=30°.
∴　　∠A=2∠B=60°.
(2)△ACD,△BCD都是“友爱三角形”.理由如下:
∵　　CD⊥AB,
∴　　∠ADC=∠BDC=90°.
在Rt△ACD中,∠A=60°,
∴　　∠ACD=90°−∠A=30°.
∴　　∠ACD= $\frac{1}{2}$∠A.
∴　　∠ACD与∠A互为“友爱角”,△ACD是“友爱三角形”.
在Rt△BCD中,∠B=30°,
∴　　∠BCD=90°−∠B=60°.
∴　　∠B= $\frac{1}{2}$∠BCD.
∴　　∠BCD与∠B互为“友爱角”,△BCD是“友爱三角形”.
综上,△ACD,△BCD都是“友爱三角形”.