第74页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
8. 如图, $ CD $ 是 $ \triangle ABC $ 的边 $ AB $ 上的高, 且 $ AB = AC $. 分别以点 $ A,C $ 为圆心, 以大于 $ \frac{1}{2}AC $ 的长为半径作弧, 两弧的交点为 $ M,N $, 直线 $ MN $ 恰好经过点 $ D $, 则 $ \angle BCD $ 的度数为 【
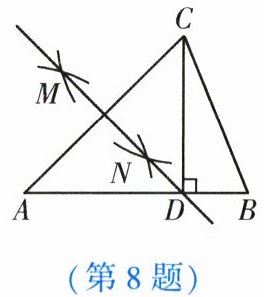
A.$ 22.5^{\circ} $
B.$ 23^{\circ} $
C.$ 23.5^{\circ} $
D.$ 24^{\circ} $
A
】
A.$ 22.5^{\circ} $
B.$ 23^{\circ} $
C.$ 23.5^{\circ} $
D.$ 24^{\circ} $
答案:
A
9. 如图, 已知 $ \angle ABC = 60^{\circ} $, 点 $ P $ 在边 $ AB $ 上, $ BP = 10 $, 点 $ E,F $ 在边 $ BC $ 上, $ PE = PF $. 若 $ BE = 2 $, 则 $ EF $ 的长为 【
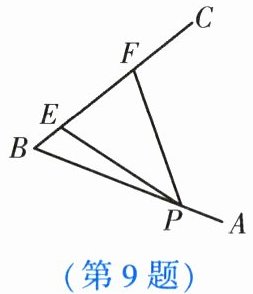
A.$ 6 $
B.$ 5 $
C.$ 4 $
D.$ 3 $
A
】
A.$ 6 $
B.$ 5 $
C.$ 4 $
D.$ 3 $
答案:
A
10. 如图, 在 $ \triangle ABC $ 中, $ \angle ABC $ 的平分线和 $ \angle ACB $ 的平分线相交于点 $ O $, 过点 $ O $ 作 $ EF // BC $ 交 $ AB $ 于点 $ E $, 交 $ AC $ 于点 $ F $, 过点 $ O $ 作 $ OD \perp AC $ 于点 $ D $. 有下列结论: ①点 $ O $ 到 $ \triangle ABC $ 各边的距离相等; ② $ EF = BE + CF $; ③ $ \angle BOC = 90^{\circ} + \frac{1}{2} \angle A $; ④设 $ OD = m, AE + AF = n $, 则 $ S_{\triangle AEF} = \frac{1}{2}mn $. 其中正确的结论是 【

A.①②③④
B.①②③
C.①③
D.①②④
A
】
A.①②③④
B.①②③
C.①③
D.①②④
答案:
A
11. 如图, 四边形 $ ABCD $ 是轴对称图形, 对称轴是直线 $ AC $, 若 $ \angle BAD = 116^{\circ} $, 则 $ \angle BAC $ 的度数为

$58^{\circ}$
.
答案:
$58^{\circ}$
12. 在平面直角坐标系中, 若点 $ P(-1,-2) $ 与点 $ Q $ 关于 $ x $ 轴对称, 则点 $ Q $ 的坐标是
$(-1,2)$
.
答案:
$(-1,2)$
13. 如图, 线段 $ BE $ 与线段 $ AC $ 互相垂直平分, 相交于点 $ D $. 若 $ \angle E = 26^{\circ} $, 则 $ \angle ABC $ 的度数为

$52^{\circ}$
.
答案:
$52^{\circ}$
14. 如图, 在等边三角形 $ ABC $ 中, $ D $ 为 $ AC $ 的中点, $ DE \perp BC $ 于点 $ E, CE = 6 $, 则线段 $ BE $ 的长为

18
.
答案:
18
15. 如图, 等边三角形 $ ABC $ 的边长为 $ 12 $, $ D $ 为边 $ AC $ 上一动点, $ E $ 为 $ AB $ 的延长线上一动点, $ DE $ 交 $ CB $ 于点 $ P $, 且 $ P $ 为 $ DE $ 的中点. 若 $ DE \perp AC $, 则 $ AE $ 的长为____

16
.
答案:
16
查看更多完整答案,请扫码查看


