《2025年基础训练大象出版社八年级数学上册人教版》

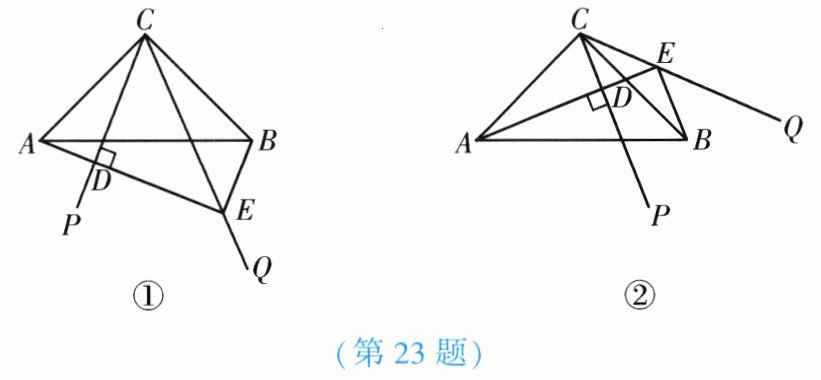
23. (12分)如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = BC$,$\angle PCQ = 45^{\circ}$,把$\triangle PCQ绕点C$旋转,在整个旋转过程中,过点$A作AD\perp CP于点D$,直线$AD交CQ于点E$.
(1)如图①,当$\angle PCQ在\angle ACB$的内部时,求证:$AD + BE = DE$;
(2)如图②,当$CQ在\angle ACB$的外部时,试探究线段$AD$,$BE和DE$之间的数量关系,并证明你的结论;
(3)在图①的条件下,若$CD = 18$,$S_{\triangle BCE}= 2S_{\triangle ACD}$,请直接写出$AE$的长.

答案：

(1) 如图，延长DA至点F，使$DF = DE$，连接CF.$\because AD\perp CP$,$\therefore \angle FDC = \angle EDC = 90^{\circ}$.在$\triangle CDF$和$\triangle CDE$中，$\left\{\begin{array}{l} DF = DE\\ \angle FDC = \angle EDC\\ CD = CD\end{array}\right.$$\therefore \triangle CDF \cong \triangle CDE(SAS)$.$\therefore \angle DCF = \angle DCE = \angle PCQ = 45^{\circ}$, $CF = CE$.$\therefore \angle ACD + \angle ACF = \angle DCF = 45^{\circ}$.又$\because \angle ACB = 90^{\circ}$，$\angle PCQ = 45^{\circ}$,$\therefore \angle ACD + \angle BCE = 45^{\circ}$.$\therefore \angle ACF = \angle BCE$.在$\triangle ACF$和$\triangle BCE$中，$\left\{\begin{array}{l} CF = CE\\ \angle ACF = \angle BCE\\ AC = BC\end{array}\right.$$\therefore \triangle ACF \cong \triangle BCE(SAS)$.$\therefore AF = BE$.$\therefore AD + BE = AD + AF = DF = DE$,即$AD + BE = DE$.
(2) $AD = BE + DE$. 证明如下:如图，在AD上截取$DF = DE$，连接CF.同
(1)可证明$\triangle CDF \cong \triangle CDE$.$\therefore \angle DCF = \angle DCE = \angle PCQ = 45^{\circ}$, $CF = CE$.$\therefore \angle ECF = \angle DCE + \angle DCF = 90^{\circ}$.$\therefore \angle BCE + \angle BCF = 90^{\circ}$.又$\because \angle ACB = 90^{\circ}$,$\therefore \angle ACF + \angle BCF = 90^{\circ}$.$\therefore \angle ACF = \angle BCE$.在$\triangle ACF$和$\triangle BCE$中，$\left\{\begin{array}{l} CF = CE\\ \angle ACF = \angle BCE\\ AC = BC\end{array}\right.$$\therefore \triangle ACF \cong \triangle BCE(SAS)$.$\therefore AF = BE$;$\therefore AD = AF + DF = BE + DE$,即$AD = BE + DE$.
(3) 24. 提示: 如
(1)中图，$\because \angle DCF = \angle DCE = \angle PCQ = 45^{\circ}$,$\therefore \angle ECF = 45^{\circ} + 45^{\circ} = 90^{\circ}$.$\therefore \triangle ECF$是等腰直角三角形.$\therefore CD = DF = DE = 18$.$\because S_{\triangle BCE} = 2S_{\triangle ACD}$,$\therefore AF = 2AD$.$\therefore AD = \frac{1}{1 + 2}×18 = 6$.$\therefore AE = AD + DE = 6 + 18 = 24$.