第66页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
6. 如图,$\angle AOB$是一个任意角,在边$OA$,$OB上分别取OM = ON$,移动角尺,使角尺两边相同的刻度分别与点$M$,$N$重合,则过角尺顶点$C的射线OC就是\angle AOB$的平分线,其依据是【

A.角的平分线上的点到角两边的距离相等
B.角的内部到角两边距离相等的点在角的平分线上
C.三边分别相等的两个三角形全等,全等三角形的对应角相等
D.两边和它们的夹角分别相等的两个三角形全等,全等三角形的对应角相等
C
】
A.角的平分线上的点到角两边的距离相等
B.角的内部到角两边距离相等的点在角的平分线上
C.三边分别相等的两个三角形全等,全等三角形的对应角相等
D.两边和它们的夹角分别相等的两个三角形全等,全等三角形的对应角相等
答案:
C
7. 如图,$AC = BC$,$AE = CD$,$AE\perp CE于点E$,$BD\perp CD于点D$.若$AE = 7$,$BD = 3$,则$DE$的长是【

A.$7$
B.$4$
C.$3$
D.$2$
B
】
A.$7$
B.$4$
C.$3$
D.$2$
答案:
B
8. 如图,小华站在河边的$A$处,在河对面(小华的正北方向)的$B$处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了$25步到达电线杆C$处,接着再向前走了$25步到达D$处,然后转向正南方向直行,当他看到电线塔$B$、电线杆$C$与所处位置在一条直线上时,他共计走了$100$步.若小华步长约为$0.4\mathrm{m}$,则$A处与电线塔B$的距离约为【
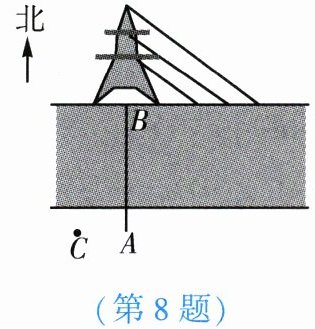
A.$20\mathrm{m}$
B.$22\mathrm{m}$
C.$25\mathrm{m}$
D.$30\mathrm{m}$
A
】
A.$20\mathrm{m}$
B.$22\mathrm{m}$
C.$25\mathrm{m}$
D.$30\mathrm{m}$
答案:
A
9. 如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle B = 30^{\circ}$,以点$A$为圆心,任意长为半径作弧,分别交$AB$,$AC于点M$,$N$,再分别以$M$,$N$为圆心,大于$\dfrac{1}{2}MN$的长为半径作弧,两弧交于点$P$,连接$AP并延长交BC于点D$.有下列结论:①$AD是\angle BAC$的平分线;②点$D在AB$的垂直平分线上;③$\angle ADC = 60^{\circ}$;④$S_{\triangle ACD}:S_{\triangle ABD}= 1:2$.其中正确的有【
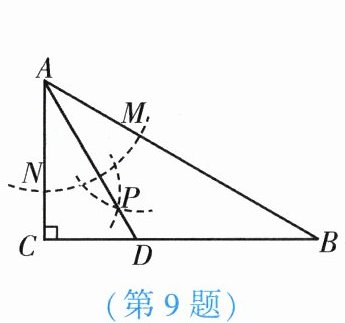
A.$1$个
B.$2$个
C.$3$个
D.$4$个
D
】
A.$1$个
B.$2$个
C.$3$个
D.$4$个
答案:
D
10. 如图,在$\triangle ABC和\triangle ADE$中,$\angle CAB= \angle DAE = 36^{\circ}$,$AB = AC$,$AD = AE$,连接$CD$,$BE$,延长$BE分别交AC$,$AD于点F$,$G$.若$BE恰好平分\angle ABC$,则下列结论错误的是【
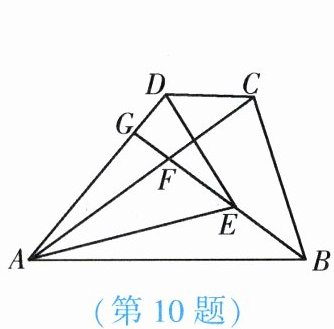
A.$\angle ADC= \angle AEB$
B.$CD// AB$
C.$DE = GE$
D.$CD = BE$
C
】
A.$\angle ADC= \angle AEB$
B.$CD// AB$
C.$DE = GE$
D.$CD = BE$
答案:
C
11. 如图,若$D为BC$的中点,则用“$SSS$”判定$\triangle ABD\cong\triangle ACD$需添加的一个条件是
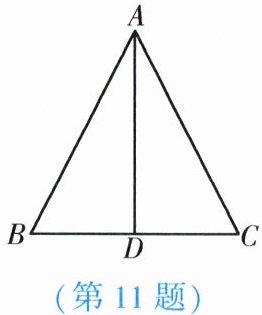
$AB = AC$
.
答案:
$AB = AC$
查看更多完整答案,请扫码查看


