《2025年基础训练大象出版社八年级数学上册人教版》

23. (11分)在△ABC中,∠B= ∠C,点D在边BC上,点E在AC上,连接DE,∠ADE= ∠AED.
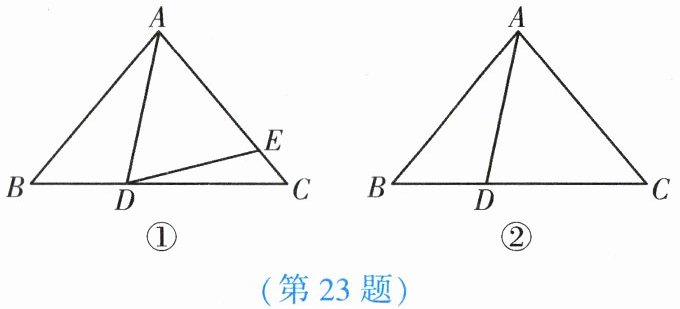
(1)如图①,当点D在边BC(不与点B,C重合)上运动,且点E在边AC上时.
①【计算发现】若∠B= 50°,∠ADE= 64°,则∠BAD的度数为28°,∠CDE的度数为14°;
②【猜想验证】猜想∠BAD与∠CDE的数量关系,并证明你的猜想.
(2)【拓展思考】如图②,当点D在边BC(不与点B,C重合)上运动,点E在边AC所在的直线上时,若∠BAD= 30°,求∠CDE的度数.

(1)②∠BAD=2∠CDE.证明如下:如图,∠B=∠C,∠4=∠3.
∵ ∠1+∠B=∠4+∠2,∠4=∠3=∠2+∠C=∠2+∠B,
∴ ∠1+∠B=∠4+∠2=∠2+∠B+∠2.
∴ ∠1=2∠2.
∴ ∠BAD=2∠CDE.
(2)如图.情况① 由条件可知,∠CDE= $\frac{1}{2}$∠BAD=$\frac{30°}{2}$=15°,
∴ ∠CDE=15°.情况② 如图,∠ADE'=∠AE'D.
∵ ∠ADC=∠B+∠BAD,∠BAE'=∠B+∠C=2∠B,∠ADE'+∠AE'D+∠DAE'=180°,
∴ 2∠ADE'+∠BAE'+∠BAD=2∠ADE'+2∠B+∠BAD=180°.
∴ ∠ADE'+∠B= $\frac{180°-∠BAD}{2}$.
∵ ∠CDE'=∠ADE'+∠ADC=∠ADE'+∠B+∠BAD,
∴ ∠CDE'= $\frac{180°-∠BAD}{2}$+∠BAD=$\frac{180°-30°}{2}$+30°=105°.综上所述,∠CDE的度数为15°或105°.

答案：
(1)①28° 14°②∠BAD=2∠CDE.证明如下:如图,∠B=∠C,∠4=∠3.
∵ ∠1+∠B=∠4+∠2,∠4=∠3=∠2+∠C=∠2+∠B,
∴ ∠1+∠B=∠4+∠2=∠2+∠B+∠2.
∴ ∠1=2∠2.
∴ ∠BAD=2∠CDE.
(2)如图.情况① 由条件可知,∠CDE= $\frac{1}{2}$∠BAD=$\frac{30°}{2}$=15°,
∴ ∠CDE=15°.情况② 如图,∠ADE'=∠AE'D.
∵ ∠ADC=∠B+∠BAD,∠BAE'=∠B+∠C=2∠B,∠ADE'+∠AE'D+∠DAE'=180°,
∴ 2∠ADE'+∠BAE'+∠BAD=2∠ADE'+2∠B+∠BAD=180°.
∴ ∠ADE'+∠B= $\frac{180°-∠BAD}{2}$.
∵ ∠CDE'=∠ADE'+∠ADC=∠ADE'+∠B+∠BAD,
∴ ∠CDE'= $\frac{180°-∠BAD}{2}$+∠BAD=$\frac{180°-30°}{2}$+30°=105°.综上所述,∠CDE的度数为15°或105°.