《2025年基础训练大象出版社八年级数学上册人教版》

21. (10分)(1)如图①,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B= 30°,∠C= 50°,求∠DAE的度数.
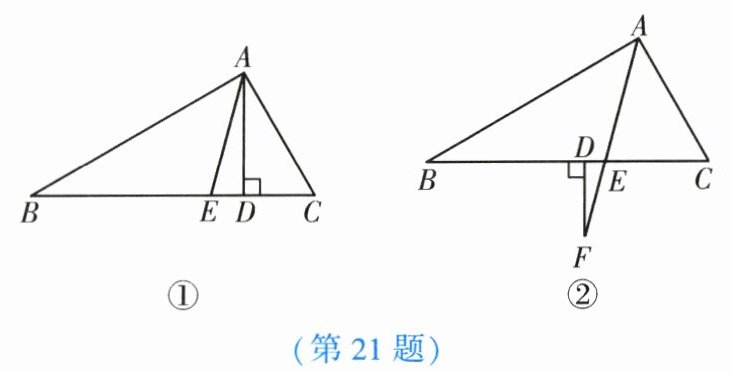
(2)如图②,已知AF平分∠BAC,交边BC于点E,延长AE至点F,过点F作FD⊥BC于点D.若∠B= x°,∠C= (x+30)°:
①∠CAE的度数为(75-x)°(含x的代数式表示);
②求∠F的度数.

答案：
(1)
∵ ∠B=30°,∠C=50°,
∴ 在△ABC中,∠BAC=180°-∠B-∠C=180°-30°-50°=100°.
∵ AE是△ABC的角平分线,
∴ ∠CAE= $\frac{1}{2}$∠BAC= $\frac{1}{2}$×100°=50°.
∵ AD是△ABC的高,
∴ ∠ADC=90°.
∴ ∠CAD=90°-∠C=90°-50°=40°.
∴ ∠DAE=∠CAE-∠CAD=50°-40°=10°.
(2)①(75-x)°②
∵ AF平分∠BAC,
∴ ∠BAE=∠CAE=(75-x)°.
∵ ∠AEC是△ABE的一个外角,
∴ ∠AEC=∠BAE+∠B=(75-x)°+x°=75°.
∴ ∠FED=∠AEC=75°.
∵ FD⊥BC,
∴ 在Rt△EDF中,∠F=90°-∠FED=90°-75°=15°.