2025年练习与测试六年级数学上册苏教版培优版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年练习与测试六年级数学上册苏教版培优版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
1. 常用的体积单位有(
立方米
)、(立方分米
)和(立方厘米
)。计量液体的体积,通常用(升
)和(毫升
)作单位。
答案:
立方米、立方分米、立方厘米;升、毫升
2. 在括号里填合适的体积或容积单位。
(1) 一瓶眼药水的容积约为 10(
(2) 一个粉笔盒的体积约为 1(
(3) 一个鱼缸的容积约为 120(
(4) 一台冰箱的容积约为 400(
(1) 一瓶眼药水的容积约为 10(
mL
)。(2) 一个粉笔盒的体积约为 1(
$dm^3$
)。(3) 一个鱼缸的容积约为 120(
L
)。(4) 一台冰箱的容积约为 400(
L
)。
答案:
(1) mL
(2) $dm^3$
(3) L
(4) L
(1) mL
(2) $dm^3$
(3) L
(4) L
3. 下面的物体都是由若干个 1 立方厘米的小正方体摆成的,它们的体积各是多少立方厘米?在括号里填一填。

(

(
10
)$cm^3$ (10
)$cm^3$ (15
)$cm^3$
答案:
10 10 15
4. 把 8 个同样大的小正方体分别放入下面两个长方体盒子中,(
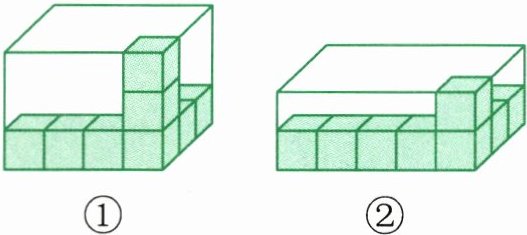
①
)号长方体盒子的容积大。
答案:
①
5. 将下图中未拆封的整瓶饮料浸没在长方体容器中,容器中上升的水的体积可能是(
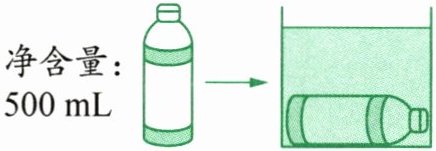
A.400
B.500
C.550
C
)毫升。
A.400
B.500
C.550
答案:
C
6. 家里来客人了,萱萱拿出一瓶果汁(如图)招待客人。她将这瓶果汁倒入同样大的小玻璃杯,倒满 5 杯后还剩 0.15 升。每个小玻璃杯的容量是多少升?


答案:
解:设每个小玻璃杯的容量是$x$升。
$5x + 0.15 = 1.15$
$5x = 1.15 - 0.15$
$5x = 1$
$x = 0.2$
答:每个小玻璃杯的容量是$0.2$升。
$5x + 0.15 = 1.15$
$5x = 1.15 - 0.15$
$5x = 1$
$x = 0.2$
答:每个小玻璃杯的容量是$0.2$升。
7. 在容器中放入不同数量的大、小球后,水溢出的情况如下。

每个小球的体积是多少立方厘米?每个大球呢?

每个小球的体积是多少立方厘米?每个大球呢?
答案:
设每个大球体积为$ V_{大} $,每个小球体积为$ V_{小} $。
由题意知:
1个大球+1个小球体积和为21 cm³(21 mL=21 cm³),即$ V_{大}+V_{小}=21 $;
1个大球+3个小球体积和为31 cm³(31 mL=31 cm³),即$ V_{大}+3V_{小}=31 $。
两式相减:$ (V_{大}+3V_{小})-(V_{大}+V_{小})=31-21 $,
化简得$ 2V_{小}=10 $,解得$ V_{小}=5 \, cm^3 $。
代入$ V_{大}+V_{小}=21 $,得$ V_{大}=21-5=16 \, cm^3 $。
每个小球体积是5立方厘米,每个大球体积是16立方厘米。
由题意知:
1个大球+1个小球体积和为21 cm³(21 mL=21 cm³),即$ V_{大}+V_{小}=21 $;
1个大球+3个小球体积和为31 cm³(31 mL=31 cm³),即$ V_{大}+3V_{小}=31 $。
两式相减:$ (V_{大}+3V_{小})-(V_{大}+V_{小})=31-21 $,
化简得$ 2V_{小}=10 $,解得$ V_{小}=5 \, cm^3 $。
代入$ V_{大}+V_{小}=21 $,得$ V_{大}=21-5=16 \, cm^3 $。
每个小球体积是5立方厘米,每个大球体积是16立方厘米。
8. 小华用若干个 1 立方厘米的正方体积木摆出一个物体,下面是从不同方向看到的图形。这个物体的体积是多少立方厘米?
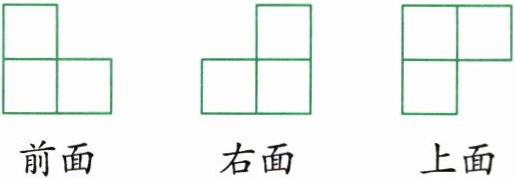

答案:
从前面看(主视图):有2列,左列高度2,右列高度1。
从右面看(右视图):有2行,后行高度2,前行高度1。
从上面看(俯视图):底层分布为(1,1)、(1,2)、(2,1)三个位置(行1列1、行1列2、行2列1)。
分析各位置高度:
(1,1):主视左列≤2,右视前行≤1,高度=1;
(1,2):主视右列≤1,右视前行≤1,高度=1;
(2,1):主视左列≤2,右视后行≤2,高度=2。
总个数:1+1+2=4。
体积=4×1=4立方厘米。
答案:4
从右面看(右视图):有2行,后行高度2,前行高度1。
从上面看(俯视图):底层分布为(1,1)、(1,2)、(2,1)三个位置(行1列1、行1列2、行2列1)。
分析各位置高度:
(1,1):主视左列≤2,右视前行≤1,高度=1;
(1,2):主视右列≤1,右视前行≤1,高度=1;
(2,1):主视左列≤2,右视后行≤2,高度=2。
总个数:1+1+2=4。
体积=4×1=4立方厘米。
答案:4
查看更多完整答案,请扫码查看


