第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 如图是由6个小正方形组成的,已知三角形A的面积是$4cm^2,$则三角形B的面积是(
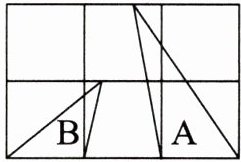
2
)$cm^2。$
答案:
2
2. 一个平行四边形和一个三角形等高等面积,已知三角形的底是8.4厘米,则平行四边形的底是(
4.2
)厘米。
答案:
4.2 【解析】等高等面积的三角形和平行四边形,三角形的底是平行四边形底的2倍。
3. 一个梯形的面积是15平方厘米,若高不变,上底和下底均扩大到原来的2倍,则梯形这时的面积是(
30
)平方厘米。
答案:
30
4. 把一个四边都是6厘米的平行四边形拉成一个正方形后,面积增加了8.4平方厘米,原来平行四边形的高是(
4.6
)厘米。
答案:
4.6
5. 新考向 数学文化 在研究平面图形的面积时,我们经常用到割补法。割补法在我国古代数学著作中被称为出入相补(又称以盈补虚)原理,它是中国数学中用于推证几何图形的面积或体积的基本原理。最早由数学家刘徽提出。其中《九章算术》的“方田章”中记载:“圭田术曰,半广以乘正从。”描述的就是三角形的面积。如图,把三角形转化成长方形,面积(

不变
)(填“变”或“不变”),长方形的长相当于三角形的(高
),长方形的宽相当于三角形的(底的一半
),长方形的面积等于(长×宽
),从而推导出三角形的面积等于(高×(底÷2)
)。
答案:
不变 高 底的一半 长×宽 高×(底÷2)
6. 如图,长度是26.25cm的高对应的底边是(

A.30cm
B.24cm
C.21cm
D.无法确定
B
)。
A.30cm
B.24cm
C.21cm
D.无法确定
答案:
B
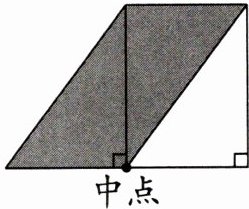
7. 把一个平行四边形按下图所示的方法剪开后(M、N是左、右两边的中点),再拼成一个新的平行四边形。关于平行四边形周长和面积的变化,下面说法正确的是(

A.周长和面积都变大
B.周长和面积都变小
C.周长不变,面积变大
D.周长变大,面积不变
D
)。
A.周长和面积都变大
B.周长和面积都变小
C.周长不变,面积变大
D.周长变大,面积不变
答案:
D
8. 如图所示的两个三角形的面积相比,甲(
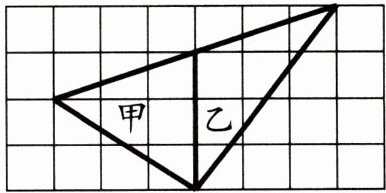
A.等于
B.大于
C.小于
D.无法比较
A
)乙。
A.等于
B.大于
C.小于
D.无法比较
答案:
A
9. 如图,已知梯形的面积是$72cm^2,$高是8cm,平行四边形(涂色部分)的面积是(
A.8
B.12
C.24
D.48
48
)$cm^2。$
A.8
B.12
C.24
D.48
答案:
D 【解析】由图可知,空白三角形和平行四边形等底等高,所以空白三角形面积是平行四边形面积的一半,即将梯形面积平均分成3份,其中2份是涂色部分面积,所以涂色部分面积为72÷3×2=48(cm²)。
查看更多完整答案,请扫码查看


