第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 行政广场有一个面积为50平方米的平行四边形月季花坛,已知该花坛的高是4米,这个花坛的底是多少米?
答案:
50÷4=12.5(米)
答:这个花坛的底是12.5米。
答:这个花坛的底是12.5米。
2. 下面的方格纸中每个小方格都是边长1厘米的小正方形。

(1) 在上面的方格纸上以 $ AB $ 为底边,画一个面积为12平方厘米的平行四边形。
(2) 再画一个与它面积相同但形状不同的平行四边形。

(1) 在上面的方格纸上以 $ AB $ 为底边,画一个面积为12平方厘米的平行四边形。
(2) 再画一个与它面积相同但形状不同的平行四边形。
答案:

(答案不唯一)

(答案不唯一)
3. 一个平行四边形,如果底不变,高增加6厘米,那么面积增加54平方厘米;如果高不变,底增加4厘米,那么面积增加22.4平方厘米。平行四边形的面积是多少平方厘米?
答案:
54÷6=9(厘米)
22.4÷4=5.6(厘米)
9×5.6=50.4(平方厘米)
答:平行四边形的面积是50.4平方厘米。
22.4÷4=5.6(厘米)
9×5.6=50.4(平方厘米)
答:平行四边形的面积是50.4平方厘米。
4. 下图中每个大正方形边长都是10 cm,小正方形边长都是5 cm。两个图中平行四边形面积分别是多少平方厘米?
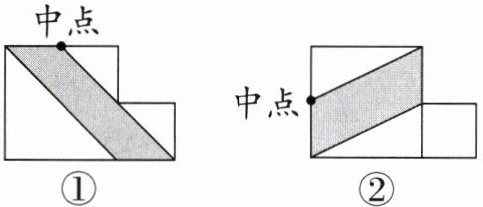

答案:
①5×10=50(cm²)
②10÷2×10=50(cm²)
答:两个图中平行四边形面积都是50 cm²。
②10÷2×10=50(cm²)
答:两个图中平行四边形面积都是50 cm²。
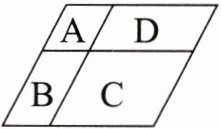
5. 将一个大平行四边形分成如图的四个小平行四边形。
(1) 用你自己喜欢的方式比较 $ S_{A} × S_{C} $ 和 $ S_{B} × S_{D} $ 的大小。
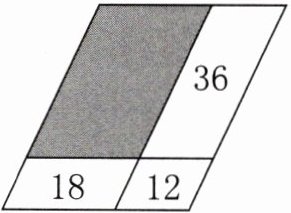
(2) 用上面的结论计算图中阴影部分的面积。(单位:$ cm^{2} $)
(1) 用你自己喜欢的方式比较 $ S_{A} × S_{C} $ 和 $ S_{B} × S_{D} $ 的大小。

(2) 用上面的结论计算图中阴影部分的面积。(单位:$ cm^{2} $)

答案:
(1)假设平行四边形A的底边为1,平行四边形D的底边为2,它们的高为1;平行四边形B和平行四边形C的高为2,则S_A=1×1=1,S_B=2×1=2,S_C=2×2=4,S_D=1×2=2,S_A×S_C=1×4=4,S_B×S_D=2×2=4,所以S_A×S_C等于S_B×S_D。(方式不唯一)
(2)18×36÷12=54(cm²)
答:图中阴影部分的面积是54 cm²。
[解析]
(1)可以分别设4个平行四边形的底和高,然后利用公式计算出面积,并验证即可;在这里要注意的是A、B等底不等高,B、C等高不等底;
(2)根据
(1)题得出的结论直接应用即可。
(1)假设平行四边形A的底边为1,平行四边形D的底边为2,它们的高为1;平行四边形B和平行四边形C的高为2,则S_A=1×1=1,S_B=2×1=2,S_C=2×2=4,S_D=1×2=2,S_A×S_C=1×4=4,S_B×S_D=2×2=4,所以S_A×S_C等于S_B×S_D。(方式不唯一)
(2)18×36÷12=54(cm²)
答:图中阴影部分的面积是54 cm²。
[解析]
(1)可以分别设4个平行四边形的底和高,然后利用公式计算出面积,并验证即可;在这里要注意的是A、B等底不等高,B、C等高不等底;
(2)根据
(1)题得出的结论直接应用即可。
查看更多完整答案,请扫码查看


