第66页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 额定电压与额定功率
| | 额定功率 | 实际功率 |
| 区别 | 概念 | 用电器在额定电压下工作时的电功率 | 用电器在实际电压下工作时的电功率 |
| | 是否变化 | 是确定的、唯一的,不随实际工作电压的改变而改变 | 是不确定的,随用电器两端所加电压的改变而改变 |
| 联系 | 当用电器两端的实际电压等于额定电压时,用电器的实际功率等于额定功率 |

当 $ U_{实} = U_{额} $ 时,$ P_{实} $______$ P_{额} $;用电器正常工作。
当 $ U_{实} > U_{额} $ 时,$ P_{实} $______$ P_{额} $;用电器超负荷工作,可能损坏用电器。
当 $ U_{实} < U_{额} $ 时,$ P_{实} $______$ P_{额} $;用电器不能正常工作,不会损坏用电器。
| | 额定功率 | 实际功率 |
| 区别 | 概念 | 用电器在额定电压下工作时的电功率 | 用电器在实际电压下工作时的电功率 |
| | 是否变化 | 是确定的、唯一的,不随实际工作电压的改变而改变 | 是不确定的,随用电器两端所加电压的改变而改变 |
| 联系 | 当用电器两端的实际电压等于额定电压时,用电器的实际功率等于额定功率 |

当 $ U_{实} = U_{额} $ 时,$ P_{实} $______$ P_{额} $;用电器正常工作。
当 $ U_{实} > U_{额} $ 时,$ P_{实} $______$ P_{额} $;用电器超负荷工作,可能损坏用电器。
当 $ U_{实} < U_{额} $ 时,$ P_{实} $______$ P_{额} $;用电器不能正常工作,不会损坏用电器。
答案:
= > <
2. 小灯泡的亮度是由______功率来决定的(而与标称的额定功率大小无关)。______功率越大,则小灯泡越亮,反之,小灯泡越暗;实际功率相同的灯泡,无论它的额定电压是否相同,其亮度都相同。
用电器使用时一定要注意它的额定电压,只有在额定电压下用电器才能正常工作。标有“PZ 220 V 60 W”的灯泡,其中“PZ”表示普通照明的意思,“220 V 60 W”表示该灯泡的额定电压是 220 V,额定功率是 60 W。
用电器使用时一定要注意它的额定电压,只有在额定电压下用电器才能正常工作。标有“PZ 220 V 60 W”的灯泡,其中“PZ”表示普通照明的意思,“220 V 60 W”表示该灯泡的额定电压是 220 V,额定功率是 60 W。
答案:
实际 实际
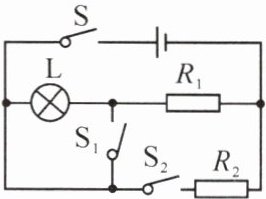
例 1 (2024·徐州)如图所示,电源电压不变,灯泡 L 标有“6 V 3 W”字样,$ R_1 $、$ R_2 $ 为定值电阻。当 S 闭合,$ S_1 $ 和 $ S_2 $ 断开时,灯泡 L 正常发光,L 和 $ R_1 $ 的功率之比为 3 : 1;当开关都闭合时,$ R_1 $ 和 $ R_2 $ 的功率之比为 4 : 1。求:
(1)灯泡 L 正常发光时的电阻;
(2)开关都闭合时 $ R_2 $ 的功率。
思路点拨 (1)根据 $ P = \frac{U^2}{R} $ 可得灯泡正常发光时的电阻;(2)当 S 闭合,$ S_1 $ 和 $ S_2 $ 断开时,灯泡 L 和 $ R_1 $ 串联,结合功率之比等于电阻之比,计算 $ R_1 $ 电阻大小,根据串联电压规律计算电源电压;当开关都闭合时,$ R_1 $ 和 $ R_2 $ 并联,结合并联电路的特点分析电阻,根据 $ P = \frac{U^2}{R} $ 计算 $ R_2 $ 的功率。
规律总结 本题考查动态电路,会识别电路的连接,会利用变形公式计算电功率。
(1)灯泡 L 正常发光时的电阻;
(2)开关都闭合时 $ R_2 $ 的功率。

思路点拨 (1)根据 $ P = \frac{U^2}{R} $ 可得灯泡正常发光时的电阻;(2)当 S 闭合,$ S_1 $ 和 $ S_2 $ 断开时,灯泡 L 和 $ R_1 $ 串联,结合功率之比等于电阻之比,计算 $ R_1 $ 电阻大小,根据串联电压规律计算电源电压;当开关都闭合时,$ R_1 $ 和 $ R_2 $ 并联,结合并联电路的特点分析电阻,根据 $ P = \frac{U^2}{R} $ 计算 $ R_2 $ 的功率。
规律总结 本题考查动态电路,会识别电路的连接,会利用变形公式计算电功率。
答案:
(1)灯泡L标有“6V 3W”,由$P=\frac{U^2}{R}$可得,灯泡的电阻为:$R_{L}=\frac{U_{L}^2}{P_{L}}=\frac{(6\ V)^2}{3\ W}=12\ \Omega$;
(2)当S闭合,$S_1$和$S_2$断开时,灯泡L和$R_1$串联,根据串联电路中电流相等,$P=UI$知,电压之比等于功率之比,为3∶1,灯泡正常发光且电压为6V,则电阻$R_1$的电压为2V;电源电压$U=U_{L}+U_1=6\ V+2\ V=8\ V$;根据$P=UI=I^2R$知,电功率之比等于电阻之比,故电阻之比为3∶1,则$R_1=\frac{1}{3}R_{L}=\frac{1}{3}×12\ \Omega=4\ \Omega$;当开关都闭合时,L被短路,$R_1$和$R_2$并联,根据$P=\frac{U^2}{R}$,电功率之比等于电阻倒数的比,$R_1$和$R_2$的功率之比为4∶1,电阻之比为1∶4,故$R_2=4R_1=4×4\ \Omega=16\ \Omega$;结合并联电路的特点分析,根据$P=\frac{U^2}{R}$计算$R_2$的功率,则$R_2$的功率$P_2=\frac{U_{电源}^2}{R_2}=\frac{(8\ V)^2}{16\ \Omega}=4\ W$。
(1)灯泡L标有“6V 3W”,由$P=\frac{U^2}{R}$可得,灯泡的电阻为:$R_{L}=\frac{U_{L}^2}{P_{L}}=\frac{(6\ V)^2}{3\ W}=12\ \Omega$;
(2)当S闭合,$S_1$和$S_2$断开时,灯泡L和$R_1$串联,根据串联电路中电流相等,$P=UI$知,电压之比等于功率之比,为3∶1,灯泡正常发光且电压为6V,则电阻$R_1$的电压为2V;电源电压$U=U_{L}+U_1=6\ V+2\ V=8\ V$;根据$P=UI=I^2R$知,电功率之比等于电阻之比,故电阻之比为3∶1,则$R_1=\frac{1}{3}R_{L}=\frac{1}{3}×12\ \Omega=4\ \Omega$;当开关都闭合时,L被短路,$R_1$和$R_2$并联,根据$P=\frac{U^2}{R}$,电功率之比等于电阻倒数的比,$R_1$和$R_2$的功率之比为4∶1,电阻之比为1∶4,故$R_2=4R_1=4×4\ \Omega=16\ \Omega$;结合并联电路的特点分析,根据$P=\frac{U^2}{R}$计算$R_2$的功率,则$R_2$的功率$P_2=\frac{U_{电源}^2}{R_2}=\frac{(8\ V)^2}{16\ \Omega}=4\ W$。
查看更多完整答案,请扫码查看


