第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
8. (1)已知 $|a| = 3$,则 $a = $____;
(2)____的绝对值是 6;
(3)若 $|x| = |-2.5|$,则 $x = $____。
(2)____的绝对值是 6;
(3)若 $|x| = |-2.5|$,则 $x = $____。
答案:
(1)±3
(2)±6
(3)±2.5
(1)±3
(2)±6
(3)±2.5
9. 在 $\frac{22}{7}$,$-(-1)$,$-|8 - 2^{2}|$,$-3$,$-3^{2}$,$-(-\frac{1}{3})^{3}$,0 中,有理数有 $m$ 个,自然数有 $n$ 个,分数有 $k$ 个,负数有 $t$ 个,则 $m - n - k + t$的值为____。
答案:
6
10. (1)若 $|a - 2| + |3 - 3b| = 0$,求 $a + 3b$的值。
(2)若 $|x - 3|$与 $|2y - 2|$互为相反数,求 $|2x - 3y|$的值。
(3)当 $m$ 取何值时,式子 $8 - |m - 5|$有最大值?最大值是多少?
(2)若 $|x - 3|$与 $|2y - 2|$互为相反数,求 $|2x - 3y|$的值。
(3)当 $m$ 取何值时,式子 $8 - |m - 5|$有最大值?最大值是多少?
答案:
(1)5.
(2)3.
(3)当m=5时,式子有最大值,为8.
(1)5.
(2)3.
(3)当m=5时,式子有最大值,为8.
11. 数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,是“数形结合”的基础。
【阅读】$|3 - 1|$表示 3 与 1 的差的绝对值,也可理解为 3 与 1 两数在数轴上所对应的两点之间的距离;$|3 + 1|$可以看作 $|3 - (-1)|$,表示 3 与 -1 的差的绝对值,也可理解为 3 与 -1 两数在数轴上所对应的两点之间的距离。
【探索】(1)$|3 - (-1)| = $____。
(2)利用如图所示数轴,解答下列问题。
①若 $|x - (-1)| = 3$,则 $x = $____;
②若 $|x - \frac{1}{2}| = |x + 3|$,则 $x = $____。
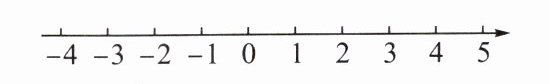
【阅读】$|3 - 1|$表示 3 与 1 的差的绝对值,也可理解为 3 与 1 两数在数轴上所对应的两点之间的距离;$|3 + 1|$可以看作 $|3 - (-1)|$,表示 3 与 -1 的差的绝对值,也可理解为 3 与 -1 两数在数轴上所对应的两点之间的距离。
【探索】(1)$|3 - (-1)| = $____。
(2)利用如图所示数轴,解答下列问题。
①若 $|x - (-1)| = 3$,则 $x = $____;
②若 $|x - \frac{1}{2}| = |x + 3|$,则 $x = $____。
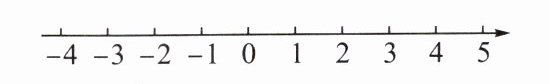
答案:
(1)4
(2)①2或-4 ②$-\dfrac{5}{4}$
(1)4
(2)①2或-4 ②$-\dfrac{5}{4}$
12. 某汽车配件厂生产了一批圆形橡胶垫,从中抽取 6 个进行检验,比标准直径长的毫米数记作正数,比标准直径短的毫米数记作负数,检查结果如下(单位:mm):
|第 1 个|第 2 个|第 3 个|第 4 个|第 5 个|第 6 个|
|+0.5| -0.3| +0.15| -0.1| 0| 0.2|
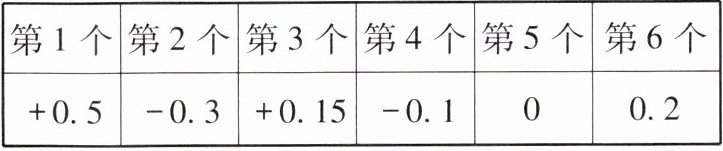
用绝对值的知识说明哪个圆形橡胶垫的质量最好。
|第 1 个|第 2 个|第 3 个|第 4 个|第 5 个|第 6 个|
|+0.5| -0.3| +0.15| -0.1| 0| 0.2|

用绝对值的知识说明哪个圆形橡胶垫的质量最好。
答案:
第5个.
13. 在解决数学问题的过程中,我们常用到分类讨论的数学思想. 下面是运用分类讨论的数学思想解决问题的过程。
【提出问题】已知三个有理数 $a$,$b$,$c$ 满足 $abc > 0$,求 $\frac{|a|}{a} + \frac{|b|}{b} + \frac{|c|}{c}$的值。
【解决问题】解:由题意知,$a$,$b$,$c$ 三个有理数都为正数或其中一个为正数,另外两个为负数。
①$a$,$b$,$c$ 都是正数,即当 $a > 0$,$b > 0$,$c > 0$时,有 $\frac{|a|}{a} + \frac{|b|}{b} + \frac{|c|}{c} = \frac{a}{a} + \frac{b}{b} + \frac{c}{c} = 1 + 1 + 1 = 3$;
②当 $a$,$b$,$c$ 中有一个为正数,另外两个为负数时,不妨设 $a > 0$,$b < 0$,$c < 0$,则 $\frac{|a|}{a} + \frac{|b|}{b} + \frac{|c|}{c} = \frac{a}{a} + \frac{-b}{b} + \frac{-c}{c} = 1 + (-1) + (-1) = -1$。
综上所述,$\frac{|a|}{a} + \frac{|b|}{b} + \frac{|c|}{c}$的值为 3 或 -1。
【探究】请根据上面的解题思路解答问题:
若三个有理数 $a$,$b$,$c$ 满足 $abc < 0$,求 $\frac{|a|}{a} + \frac{|b|}{b} + \frac{|c|}{c}$的值。
【提出问题】已知三个有理数 $a$,$b$,$c$ 满足 $abc > 0$,求 $\frac{|a|}{a} + \frac{|b|}{b} + \frac{|c|}{c}$的值。
【解决问题】解:由题意知,$a$,$b$,$c$ 三个有理数都为正数或其中一个为正数,另外两个为负数。
①$a$,$b$,$c$ 都是正数,即当 $a > 0$,$b > 0$,$c > 0$时,有 $\frac{|a|}{a} + \frac{|b|}{b} + \frac{|c|}{c} = \frac{a}{a} + \frac{b}{b} + \frac{c}{c} = 1 + 1 + 1 = 3$;
②当 $a$,$b$,$c$ 中有一个为正数,另外两个为负数时,不妨设 $a > 0$,$b < 0$,$c < 0$,则 $\frac{|a|}{a} + \frac{|b|}{b} + \frac{|c|}{c} = \frac{a}{a} + \frac{-b}{b} + \frac{-c}{c} = 1 + (-1) + (-1) = -1$。
综上所述,$\frac{|a|}{a} + \frac{|b|}{b} + \frac{|c|}{c}$的值为 3 或 -1。
【探究】请根据上面的解题思路解答问题:
若三个有理数 $a$,$b$,$c$ 满足 $abc < 0$,求 $\frac{|a|}{a} + \frac{|b|}{b} + \frac{|c|}{c}$的值。
答案:
1或-3.
查看更多完整答案,请扫码查看


