第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
9. 若“!”是一种运算符号,且$1!= 1$,$2!= 2×1$,$3!= 3×2×1$,$4!= 4×3×2×1$,…$$,则$100!÷98!$的值为______.
答案:
9900
10. 请你参考下面的讲解,用运算律计算:
利用运算律有时能进行简便计算.
例1.$98×12= (100-2)×12= 1200-24= 1176$;
例2.$-16×233+17×233= (-16+17)×233= 233$.

(1)$999×(-15)$;
(2)$999×118\frac{4}{5}+999×(-\frac{1}{5})-999×18\frac{3}{5}$.
利用运算律有时能进行简便计算.
例1.$98×12= (100-2)×12= 1200-24= 1176$;
例2.$-16×233+17×233= (-16+17)×233= 233$.

(1)$999×(-15)$;
(2)$999×118\frac{4}{5}+999×(-\frac{1}{5})-999×18\frac{3}{5}$.
答案:
(1)$-14985$;(2)99900.
11. 某粮食加工厂从加工的粮食中抽出20袋检查质量,以每袋50kg为标准,将超过的千克数记为正数,不足的千克数记为负数,结果记录如下:
| 差额/kg | -0.7 | -0.5 | -0.2 | 0 | +0.4 | +0.5 | +0.7 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 袋数 | 1 | 3 | 4 | 5 | 3 | 3 | 1 |
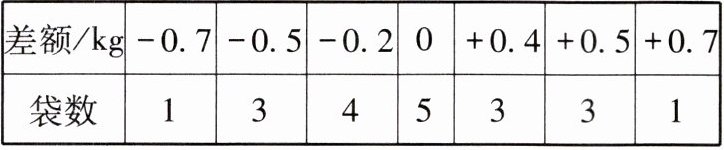
这20袋大米共超重或不足多少千克?总质量为多少千克?
| 差额/kg | -0.7 | -0.5 | -0.2 | 0 | +0.4 | +0.5 | +0.7 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 袋数 | 1 | 3 | 4 | 5 | 3 | 3 | 1 |

这20袋大米共超重或不足多少千克?总质量为多少千克?
答案:
超重$0.4\ kg$;总质量为$1000.4\ kg$.
12. 我们知道:$\frac{1}{2}×\frac{2}{3}= \frac{1}{3}$,$\frac{1}{2}×\frac{2}{3}×\frac{3}{4}= \frac{1}{4}$,$\frac{1}{2}×\frac{2}{3}×\frac{3}{4}×\frac{4}{5}= \frac{1}{5}$,…$$,$\frac{1}{2}×\frac{2}{3}×\frac{3}{4}×…×\frac{n}{n+1}= \frac{1}{n+1}$.
根据上述规律解答下列问题.
(1)计算:$(\frac{1}{2}-1)(\frac{1}{3}-1)(\frac{1}{4}-1)…\cdot\cdot(\frac{1}{100}-1)$;
(2)将2020减去它的$\frac{1}{2}$,再减去余下的$\frac{1}{3}$,再减去余下的$\frac{1}{4}$,再减去余下的$\frac{1}{5}……$依次类推,直到最后减去余下的$\frac{1}{2020}$,最后的结果是多少?
根据上述规律解答下列问题.
(1)计算:$(\frac{1}{2}-1)(\frac{1}{3}-1)(\frac{1}{4}-1)…\cdot\cdot(\frac{1}{100}-1)$;
(2)将2020减去它的$\frac{1}{2}$,再减去余下的$\frac{1}{3}$,再减去余下的$\frac{1}{4}$,再减去余下的$\frac{1}{5}……$依次类推,直到最后减去余下的$\frac{1}{2020}$,最后的结果是多少?
答案:
(1)$-\frac{1}{100}$;(2)$1$.
查看更多完整答案,请扫码查看


