第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
7. 计算$(-3\frac{1}{4}) + [(+4\frac{5}{6}) + (-\frac{3}{4}) + (+2\frac{1}{6})]$的结果是( )
A.-1
B.1
C.3
D.4
A.-1
B.1
C.3
D.4
答案:
C
8. 如果$a + b + c < 0$,那么( )
A.$a$,$b$,$c$三个数中至少有两个负数
B.$a$,$b$,$c$三个数中有且只有一个负数
C.$a$,$b$,$c$三个数中至少有一个负数
D.$a$,$b$,$c$三个数中有两个是正数或有两个是负数
A.$a$,$b$,$c$三个数中至少有两个负数
B.$a$,$b$,$c$三个数中有且只有一个负数
C.$a$,$b$,$c$三个数中至少有一个负数
D.$a$,$b$,$c$三个数中有两个是正数或有两个是负数
答案:
C
9. 一只电子跳蚤从数轴原点开始,第 1 次向右跳 1 个单位长度,紧接着第 2 次向左跳 2 个单位长度,第 3 次向右跳 3 个单位长度,第 4 次向左跳 4 个单位长度……依此规律跳下去,当它跳第 100 次落下时,落点处到原点的距离是______个单位长度。
答案:
50
10. 若数轴上表示数$a$的点在 -4 与 2 之间,则$\vert a + 4\vert + \vert 2 - a\vert =$______。
答案:
6
11. 有 8 筐白菜,以每筐 25 kg 为标准,超过的千克数记作正数,不足的千克数记作负数,称重后的质量(单位:kg)记录如下:
|序号|1|2|3|4|5|6|7|8|
|记录|1.5|-3|2|-0.5|1|-2|-2|-2.5|
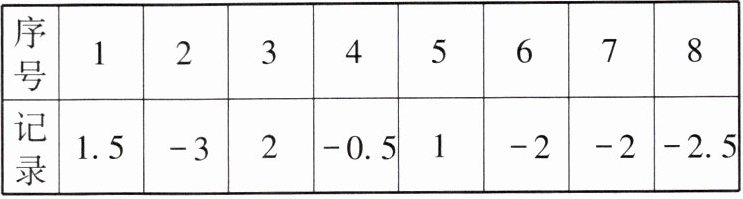
(1) 这 8 筐白菜中,最接近标准质量的 1 筐白菜的质量为多少千克?
(2) 与标准质量相比,这 8 筐白菜总计超过或不足多少千克?
(3) 若白菜每千克售价 2.6 元,则这 8 筐白菜可卖多少元?
|序号|1|2|3|4|5|6|7|8|
|记录|1.5|-3|2|-0.5|1|-2|-2|-2.5|

(1) 这 8 筐白菜中,最接近标准质量的 1 筐白菜的质量为多少千克?
(2) 与标准质量相比,这 8 筐白菜总计超过或不足多少千克?
(3) 若白菜每千克售价 2.6 元,则这 8 筐白菜可卖多少元?
答案:
(1)第4筐,24.5 kg.
(2)总计不足5.5 kg.
(3)505.7元.
(1)第4筐,24.5 kg.
(2)总计不足5.5 kg.
(3)505.7元.
12. 阅读下列材料并解答问题。
计算:$(-5\frac{5}{6}) + (-9\frac{2}{3}) + 17\frac{3}{4} + (-3\frac{1}{2})$。
解:原式$=[(-5) + (-\frac{5}{6})] + [(-9) + (-\frac{2}{3})] + (17 + \frac{3}{4}) + [(-3) + (-\frac{1}{2})]$
$=[(-5) + (-9) + 17 + (-3)] + [(-\frac{5}{6}) + (-\frac{2}{3}) + \frac{3}{4} + (-\frac{1}{2})]$
$=0 + (-1\frac{1}{4})$
$=-1\frac{1}{4}$。
上面这种解题方法叫拆项法,请仿照上面的方法计算:
(1) $-1\frac{1}{4} + (-2\frac{1}{3}) + 7\frac{5}{6} + (-4\frac{1}{2})$;
(2) $(-2019\frac{2}{3}) + 2018\frac{3}{4} + (-2017\frac{5}{6}) + 2016\frac{1}{2}$。
计算:$(-5\frac{5}{6}) + (-9\frac{2}{3}) + 17\frac{3}{4} + (-3\frac{1}{2})$。
解:原式$=[(-5) + (-\frac{5}{6})] + [(-9) + (-\frac{2}{3})] + (17 + \frac{3}{4}) + [(-3) + (-\frac{1}{2})]$
$=[(-5) + (-9) + 17 + (-3)] + [(-\frac{5}{6}) + (-\frac{2}{3}) + \frac{3}{4} + (-\frac{1}{2})]$
$=0 + (-1\frac{1}{4})$
$=-1\frac{1}{4}$。
上面这种解题方法叫拆项法,请仿照上面的方法计算:
(1) $-1\frac{1}{4} + (-2\frac{1}{3}) + 7\frac{5}{6} + (-4\frac{1}{2})$;
(2) $(-2019\frac{2}{3}) + 2018\frac{3}{4} + (-2017\frac{5}{6}) + 2016\frac{1}{2}$。
答案:
(1)$-\frac{1}{4}$;
(2)$-2\frac{1}{4}$.
(1)$-\frac{1}{4}$;
(2)$-2\frac{1}{4}$.
查看更多完整答案,请扫码查看


