第75页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
8. 某体育场一扇形区域观众席的座位按下表所列方式设置:
| 排数 | 1 | 2 | 3 | 4 |
| 座位数 | 12 | 15 | 18 | 21 |
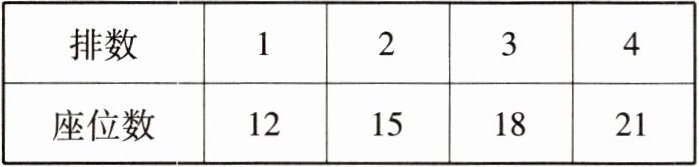
按这样的方式排列下去:
(1) 第 6 排有
(2) 小明说,他坐的那一排刚好有 100 个座位。你认为他说得对吗?请说明理由。
| 排数 | 1 | 2 | 3 | 4 |
| 座位数 | 12 | 15 | 18 | 21 |

按这样的方式排列下去:
(1) 第 6 排有
27
个座位;(2) 小明说,他坐的那一排刚好有 100 个座位。你认为他说得对吗?请说明理由。
(2)假设第$n$排有100个座位,则$3n + 9 = 100$,$3n=100 - 9$,$3n = 91$,$n=\frac{91}{3}\approx30.33$。因为排数$n$为正整数,而$\frac{91}{3}$不是整数,所以小明说得不对。
答案:
(1)
由表格可知,每排座位数比前一排多$3$,第一排有$12$个座位,所以座位数与排数的关系为$12 + 3(n - 1)=3n + 9$($n$为排数)。
当$n = 6$时,$3×6 + 9=27$。
故第$6$排有$27$个座位。
(2)
假设第$n$排有$100$个座位,则$3n + 9 = 100$,
$3n=100 - 9$,
$3n = 91$,
$n=\frac{91}{3}\approx30.33$。
因为排数$n$为正整数,而$\frac{91}{3}$不是整数,所以小明说得不对。
(1)
由表格可知,每排座位数比前一排多$3$,第一排有$12$个座位,所以座位数与排数的关系为$12 + 3(n - 1)=3n + 9$($n$为排数)。
当$n = 6$时,$3×6 + 9=27$。
故第$6$排有$27$个座位。
(2)
假设第$n$排有$100$个座位,则$3n + 9 = 100$,
$3n=100 - 9$,
$3n = 91$,
$n=\frac{91}{3}\approx30.33$。
因为排数$n$为正整数,而$\frac{91}{3}$不是整数,所以小明说得不对。
9. 观察下列两行数:
1,3,5,7,9,11,13,15,17,…$1,4,7,10,13,16,19,22,25,…$
探究发现:第 1 个相同的数是 1,第 2 个相同的数是 7,……$$ 则第 $ n $ 个相同的数是多少?
1,3,5,7,9,11,13,15,17,…$1,4,7,10,13,16,19,22,25,…$
探究发现:第 1 个相同的数是 1,第 2 个相同的数是 7,……$$ 则第 $ n $ 个相同的数是多少?
答案:
第一行数列为奇数数列,通项公式为 $a_n = 2n - 1$,其中 $n$ 为正整数。
第二行数列公差为3,首项为1,通项公式为 $b_m = 1 + 3(m - 1) = 3m - 2$,其中 $m$ 为正整数。
设第n个相同的数为x,则x同时满足 $a_k =x$ 和 $b_l = x$(k,l为某正整数),即:
$2k - 1 = 3l - 2$
化简得:
$2k = 3l - 1$
$k = \frac{3l - 1}{2}$
由于k为正整数,因此$3l - 1$必须为偶数,即l必须为奇数,设$l = 2n - 1$(n为正整数),则:
$k = \frac{3(2n - 1) - 1}{2} = \frac{6n - 3 - 1}{2} = \frac{6n - 4}{2} = 3n - 2$
将$l = 2n - 1$代入$b_l$的通项公式,得到第n个相同的数:
$x = b_{2n - 1} = 3(2n - 1) - 2 = 6n - 3 - 2 = 6n - 5$
因此第n个相同的数为$6n - 5$。
第二行数列公差为3,首项为1,通项公式为 $b_m = 1 + 3(m - 1) = 3m - 2$,其中 $m$ 为正整数。
设第n个相同的数为x,则x同时满足 $a_k =x$ 和 $b_l = x$(k,l为某正整数),即:
$2k - 1 = 3l - 2$
化简得:
$2k = 3l - 1$
$k = \frac{3l - 1}{2}$
由于k为正整数,因此$3l - 1$必须为偶数,即l必须为奇数,设$l = 2n - 1$(n为正整数),则:
$k = \frac{3(2n - 1) - 1}{2} = \frac{6n - 3 - 1}{2} = \frac{6n - 4}{2} = 3n - 2$
将$l = 2n - 1$代入$b_l$的通项公式,得到第n个相同的数:
$x = b_{2n - 1} = 3(2n - 1) - 2 = 6n - 3 - 2 = 6n - 5$
因此第n个相同的数为$6n - 5$。
10. (实际应用)某餐厅中,一张桌子可坐 6 个人,有如图 3 - 3 - 5 所示的两种摆放方式:
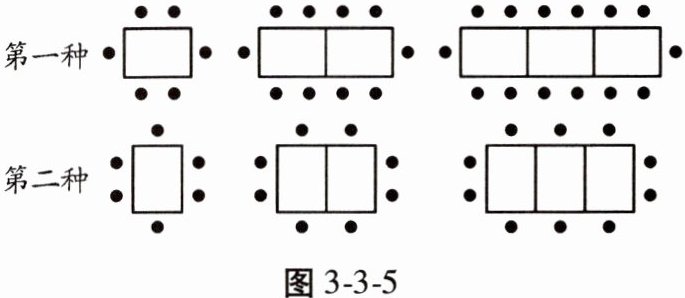
(1) 当有 5 张桌子时,两种摆放方式各能坐多少人?
(2) 某天中午这个餐厅要接待 60 位顾客共同就餐,但餐厅只有 15 张这样的餐桌,餐厅空间足够大。若你是这个餐厅的经理,你会选择哪种方式来摆放餐桌?为什么?

(1) 当有 5 张桌子时,两种摆放方式各能坐多少人?
(2) 某天中午这个餐厅要接待 60 位顾客共同就餐,但餐厅只有 15 张这样的餐桌,餐厅空间足够大。若你是这个餐厅的经理,你会选择哪种方式来摆放餐桌?为什么?
答案:
(1) 第一种摆放方式能坐 22 人,第二种摆放方式能坐 14 人。
(2) 选择第一种方式来摆放餐桌,因为第一种方式 15 张桌子能坐 62 人,可容纳 60 位顾客,而第二种方式 15 张桌子只能坐 34 人,不能容纳 60 位顾客。
(1) 第一种摆放方式能坐 22 人,第二种摆放方式能坐 14 人。
(2) 选择第一种方式来摆放餐桌,因为第一种方式 15 张桌子能坐 62 人,可容纳 60 位顾客,而第二种方式 15 张桌子只能坐 34 人,不能容纳 60 位顾客。
查看更多完整答案,请扫码查看


