《2025年绩优学案七年级数学上册北师大版》

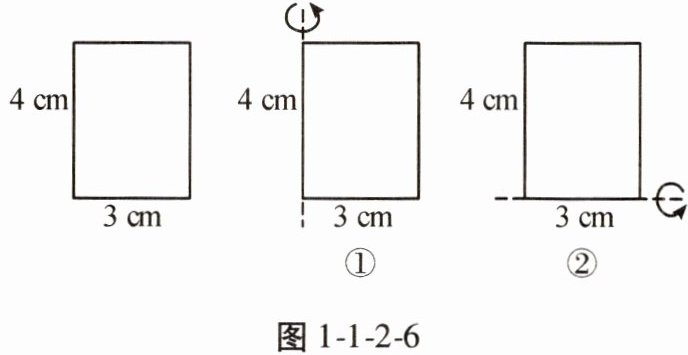
10. 图1-1-2-6是一张长为4 cm,宽为3 cm的长方形纸片,将该长方形纸片分别绕长、宽所在直线旋转一周(如图①、图②),会得到两个几何体,请你通过计算说明哪种旋转方式得到的几何体的体积大。(结果保留$\pi$)

答案： 情况①：绕长所在直线旋转
旋转轴：长（4 cm）
底面半径：宽（3 cm）
高：长（4 cm）
体积公式：$ V = \pi r^2 h $
计算：$ V_1 = \pi × 3^2 × 4 = 36\pi \, cm^3 $
情况②：绕宽所在直线旋转
旋转轴：宽（3 cm）
底面半径：长（4 cm）
高：宽（3 cm）
体积公式：$ V = \pi r^2 h $
计算：$ V_2 = \pi × 4^2 × 3 = 48\pi \, cm^3 $
比较
$ 48\pi ＞ 36\pi $，故绕宽所在直线旋转得到的几何体体积大。
结论：绕宽所在直线旋转得到的几何体体积大，体积为 $ 48\pi \, cm^3 $。

11. 小明学习了“面动成体”之后,他用一个边长分别为3 cm,4 cm和5 cm的直角三角形,绕其中一条边所在直线旋转一周,得到了一个几何体。
(1)请画出可能得到的几何体简图；
(2)分别计算出这些几何体的体积。($V_{圆锥} = \frac{1}{3}\pi r^{2}h$,结果保留$\pi$)

答案：
(1)可能得到的几何体简图：
情况一：绕长为$3cm$的边旋转，得到一个底面半径为$4cm$，高为$3cm$的圆锥。
[此处应画一个圆锥的简图，由于文本形式限制，无法直接画出，描述为：一个圆锥，底面半径标为$4cm$，高标为$3cm$]
情况二：绕长为$4cm$的边旋转，得到一个底面半径为$3cm$，高为$4cm$的圆锥。
[此处应画一个圆锥的简图，描述为：一个圆锥，底面半径标为$3cm$，高标为$4cm$]
情况三：绕长为$5cm$的边旋转，得到一个由两个共用底面半径的圆锥组成的几何体，底面半径为$\frac{12}{5}cm$（由直角三角形的面积和斜边求出，即$r=\frac{3×4}{5}=\frac{12}{5}cm$），两个圆锥的高分别为$\frac{9}{5}cm$和$\frac{16}{5}cm$（根据相似三角形求出）。
[此处应画一个由两个圆锥组成的几何体的简图，描述为：两个圆锥底面重合，一个圆锥的高标为$\frac{9}{5}cm$，另一个圆锥的高标为$\frac{16}{5}cm$，底面半径标为$\frac{12}{5}cm$]
(2)计算体积：
情况一：$V_1 = \frac{1}{3}\pi × 4^{2} × 3 = 16\pi(cm^{3})$；
情况二：$V_2 = \frac{1}{3}\pi × 3^{2} × 4 = 12\pi(cm^{3})$；
情况三：$V_3 = \frac{1}{3}\pi × (\frac{12}{5})^{2} × \frac{9}{5} + \frac{1}{3}\pi × (\frac{12}{5})^{2} × \frac{16}{5} = \frac{1}{3}\pi × (\frac{144}{25}) × 5 = \frac{48}{5}\pi = 9.6\pi × 2 ÷ 2 = 9.6\pi × (可简化为分数或小数形式，此处保留分数形式为\frac{48}{5}\pi)(cm^{3})$，
由于题目要求保留$\pi$，所以写为$\frac{48}{5}\pi cm^3$或$9.6\pi cm^3$均可，这里选择$\frac{48}{5}\pi cm^3$。
综上，可能得到的几何体的体积分别为$16\pi cm^3$，$12\pi cm^3$和$\frac{48}{5}\pi cm^3$。