《2025年同步练习册人民教育出版社八年级数学上册人教版新疆专版》

1. 以下判断正确的是(C)

A.三角形的一个外角等于两个内角的和
B.三角形的外角大于任何一个内角
C.一个三角形中,至少有一个角大于或等于 $60^{\circ}$
D.三角形的外角是内角的邻补角

答案： C

2. 若一个三角形的三个外角之比为 $3:3:4$,则这个三角形是(D)
A.等边三角形
B.等腰直角三角形
C.直角三角形
D.等腰三角形

答案： D

3. 在一个三角形的三个外角中,钝角的个数最少有(C)
A.$0$ 个
B.$1$ 个
C.$2$ 个
D.$3$ 个

答案： C

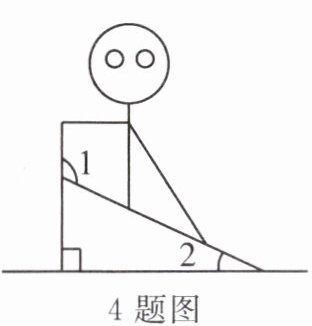
4. 体育课上的侧压腿动作可以抽象为几何图形,如图所示. 若 $\angle 1 = 115^{\circ}$,则 $\angle 2$ 的度数为25°.

答案： 25°

5. 如图,在 $\triangle ABC$ 中,$AD$ 平分 $\angle BAC$.
(1)$\angle 1$,$\angle 2$,$\angle 3$ 的大小关系为∠3＞∠2＞∠1.(用“$＞$”连接)
(2)若 $\angle 2 = 70^{\circ}$,则 $\angle 1 + \angle 3 = $140$^{\circ}$.

答案： （1）∠3＞∠2＞∠1 （2）140

6. 如图,在 $\triangle ABC$ 中,$\angle 1 = \angle 2 = \angle 3$.
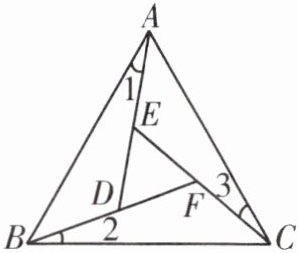
(1)求证：$\angle BAC = \angle DEF$；
(2)若 $\angle BAC = 70^{\circ}$,$\angle DFE = 50^{\circ}$,求 $\angle ABC$ 的度数.

答案： （1）证明 在△ACE中，∠DEF=∠3+∠CAE.因为∠1=∠3，所以∠DEF=∠1+∠CAE=∠BAC.即∠BAC=∠DEF.（2）解 在△BCF中，∠DFE=∠2+∠BCF.因为∠2=∠3，所以∠DFE=∠3+∠BCF.即∠DFE=∠ACB.因为∠BAC=70°，∠DFE=50°，所以在△ABC中，∠ABC=180°-∠BAC-∠ACB=180°-70°-50°=60°.