《2025年同步练习册人民教育出版社八年级数学上册人教版新疆专版》

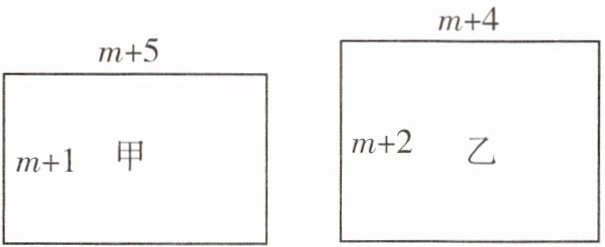
20. 甲、乙两个长方形的边长如图所示 $(m＞0)$,面积分别为 $S_{1}$,$S_{2}$。
(1)$S_{1}=$$m^2 + 6m + 5$,$S_{2}=$$m^2 + 6m + 8$；(用含 $m$ 的代数式表示,结果化为最简形式)
(2)$S_{1}$$＜$$S_{2}$；(填“$＞$”“$＜$” 或 “$=$”)
(3)若一个正方形的周长等于甲、乙两个长方形的周长之和,设该正方形的面积为 $S_{3}$,则 $S_{3}$ 与 $2(S_{1}+S_{2})$ 的差是否为定值？若为定值,则求出该值；若不为定值,则说明理由。

正方形的周长为$2×(m + 5 + m + 1 + m + 4 + m + 2)=8m + 24$. 所以正方形的边长为$(8m + 24)÷4=2m + 6$.所以$S_3=(2m + 6)^2=4m^2 + 24m + 36$.所以$S_3 - 2(S_1 + S_2)=4m^2 + 24m + 36 - 2×(m^2 + 6m + 5 + m^2 + 6m + 8)=4m^2 + 24m + 36 - 2×(2m^2 + 12m + 13)=10$.所以$S_3$与$2(S_1 + S_2)$的差是定值，定值为10.

答案： （1）$m^2 + 6m + 5$ $m^2 + 6m + 8$（2）$＜$（3）正方形的周长为$2×(m + 5 + m + 1 + m + 4 + m + 2)=8m + 24$. 所以正方形的边长为$(8m + 24)÷4=2m + 6$.所以$S_3=(2m + 6)^2=4m^2 + 24m + 36$.所以$S_3 - 2(S_1 + S_2)=4m^2 + 24m + 36 - 2×(m^2 + 6m + 5 + m^2 + 6m + 8)=4m^2 + 24m + 36 - 2×(2m^2 + 12m + 13)=10$.所以$S_3$与$2(S_1 + S_2)$的差是定值，定值为10.

21. 实践探究：某数学兴趣小组利用“等面积法”分别构造了两种图形验证“平方差公式”,如图所示。
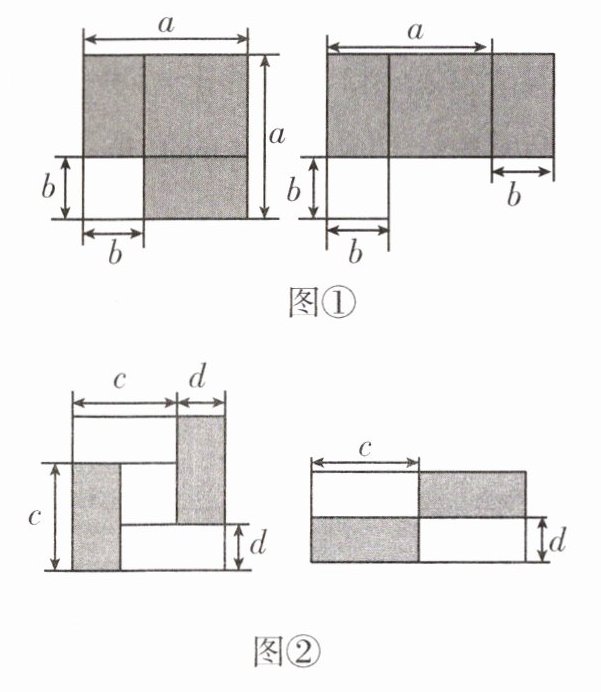
(1)探究：以下两种图形能够验证平方差公式的是①(填序号)；
(2)应用：利用“平方差公式”计算 $1949^{2}-1948×1950$；
(3)拓展：运用平方差公式计算 $(2 + 1)×(2^{2}+1)×(2^{4}+1)×(2^{8}+1)×…×(2^{1024}+1)+1$。

答案： （1）①（2）$1949^2 - 1948×1950=1949^2-(1949 - 1)×(1949 + 1)=1949^2-(1949^2 - 1)=1949^2 - 1949^2 + 1=1$.（3）原式$=(2 - 1)×(2 + 1)×(2^2 + 1)×(2^4 + 1)×(2^8 + 1)×\cdots×(2^{1024} + 1)+1=(2^2 - 1)×(2^2 + 1)×(2^4 + 1)×(2^8 + 1)×\cdots×(2^{1024} + 1)+1=(2^4 - 1)×(2^4 + 1)×(2^8 + 1)×\cdots×(2^{1024} + 1)+1=\cdots=2^{2048}-1 + 1=2^{2048}$