《2025年同步练习册人民教育出版社八年级数学上册人教版新疆专版》

如图,公园有一条 “Z” 字形道路 $AB - BC - CD$,其中 $AB // CD$,在 $E$,$M$,$F$ 处各有一个小石凳,且 $BE = CF$,$M$ 为 $BC$ 的中点,连接 $EM$,$MF$。

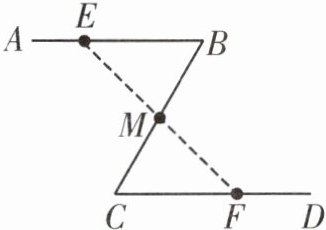
(1)石凳 $M$ 到石凳 $E$,$F$ 的距离 $ME$,$MF$ 是否相等？说出你推断的理由。
(2)$E$,$M$,$F$ 三点是否共线？请说明理由。

答案：
(1) $ME = MF$。理由如下：
因为 $AB // CD$，所以 $\angle B = \angle C$。
因为 $M$ 为 $BC$ 的中点，所以 $BM = CM$。
在 $\triangle BEM$ 和 $\triangle CFM$ 中，
$\left\{ \begin{array}{l} BE = CF, \\ \angle B = \angle C, \\ BM = CM, \end{array} \right.$
所以 $\triangle BEM \cong \triangle CFM(SAS)$，因此 $ME = MF$。
(2) $E$，$M$，$F$ 三点共线。理由如下：
因为 $\triangle BEM \cong \triangle CFM$，所以 $\angle BME = \angle CMF$。
因为 $\angle BME + \angle EMC = 180°$（平角定义），
所以 $\angle CMF + \angle EMC = 180°$，即 $\angle EMF = 180°$，
因此 $E$，$M$，$F$ 三点共线。