第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
20. 如果三角形的两个内角$\alpha与\beta满足2\alpha+\beta = 90^{\circ}$,那么我们称这样的三角形为“奇妙互余三角形”.请解决以下问题:
(1)①若$\triangle ABC$是“奇妙互余三角形”,$\angle C>90^{\circ}$,$\angle A = 60^{\circ}$,则$\angle B = $
②若$\triangle ABC$是“奇妙互余三角形”,$\angle C>90^{\circ}$,$\angle A = 40^{\circ}$,则$\angle C = $
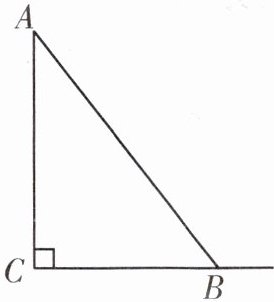
(2)如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle ABC = 52^{\circ}$,点$P是射线CB$上的一点,且$\triangle ABP$是“奇妙互余三角形”,请求出$\angle APC$的度数.
(1)①若$\triangle ABC$是“奇妙互余三角形”,$\angle C>90^{\circ}$,$\angle A = 60^{\circ}$,则$\angle B = $
15°
;②若$\triangle ABC$是“奇妙互余三角形”,$\angle C>90^{\circ}$,$\angle A = 40^{\circ}$,则$\angle C = $
115°或130°
.(2)如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle ABC = 52^{\circ}$,点$P是射线CB$上的一点,且$\triangle ABP$是“奇妙互余三角形”,请求出$\angle APC$的度数.

答案:
解(1)①15° ②115°或130°
(2)当P在线段BC上时,如图①,∠C=90°,∠ABC=52°,
当2∠PAB+∠ABC=90°时,
∠PAB=$\frac{90°-52°}{2}$=19°.
∠APC=52°+19°=71°.
当∠PAB+2∠ABC=90°时,无解.
当P在CB延长线上时,如图②,
因为∠ABC=52°,
所以∠ABP=180°-52°=128°.
当2∠APC+∠BAP=90°时,
因为∠APC+∠BAP=∠ABC,
所以∠APC=90°-∠ABC=38°.
当∠APC+2∠BAP=90°时,
因为∠APC+∠BAP=∠ABC,
所以∠BAP=90°-∠ABC=38°.
所以∠APC=52°-38°=14°.
综上所述,∠APC的度数为71°或38°或14°.
(2)当P在线段BC上时,如图①,∠C=90°,∠ABC=52°,
当2∠PAB+∠ABC=90°时,
∠PAB=$\frac{90°-52°}{2}$=19°.
∠APC=52°+19°=71°.
当∠PAB+2∠ABC=90°时,无解.
当P在CB延长线上时,如图②,
因为∠ABC=52°,
所以∠ABP=180°-52°=128°.
当2∠APC+∠BAP=90°时,
因为∠APC+∠BAP=∠ABC,
所以∠APC=90°-∠ABC=38°.
当∠APC+2∠BAP=90°时,
因为∠APC+∠BAP=∠ABC,
所以∠BAP=90°-∠ABC=38°.
所以∠APC=52°-38°=14°.
综上所述,∠APC的度数为71°或38°或14°.
21. 在$\triangle ABC$中,$AD平分\angle BAC$.
(1)如图①,$P为线段AD$上一点,过点$P作PE\perp AD交线段BC的延长线于点E$.
①若$\angle B = 30^{\circ}$,$\angle ACB = 80^{\circ}$,则$\angle E = $
②猜想$\angle E与\angle B$,$\angle ACB$之间的数量关系,并给出证明.
(2)如图②,$P在线段AD$的延长线上,过点$P作PE\perp AD交直线BC于点E$,请直接写出$\angle PED与\angle B$,$\angle C$的数量关系.
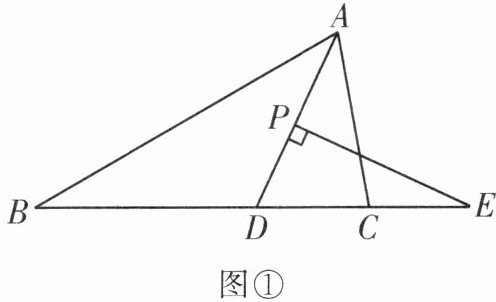
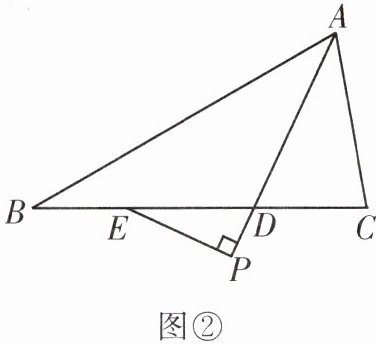
(1)如图①,$P为线段AD$上一点,过点$P作PE\perp AD交线段BC的延长线于点E$.
①若$\angle B = 30^{\circ}$,$\angle ACB = 80^{\circ}$,则$\angle E = $
25°
;②猜想$\angle E与\angle B$,$\angle ACB$之间的数量关系,并给出证明.
(2)如图②,$P在线段AD$的延长线上,过点$P作PE\perp AD交直线BC于点E$,请直接写出$\angle PED与\angle B$,$\angle C$的数量关系.


答案:
解(1)①25°
②∠E=$\frac{1}{2}$(∠ACB-∠B).证明如下:
设∠B=x,∠ACB=y,
因为AD平分∠BAC,
所以∠BAD=∠CAD=$\frac{1}{2}$∠BAC.
因为∠B+∠ACB+∠BAC=180°,
所以∠BAC=180°-x-y.
所以∠BAD=$\frac{1}{2}$(180°-x-y).
所以∠PDE=∠B+∠BAD=x+$\frac{1}{2}$(180°-x-y)=90°+$\frac{1}{2}$(x-y).
因为PE⊥AD,所以∠PDE+∠E=90°.
所以∠E=90°-[90°+$\frac{1}{2}$(x-y)]=$\frac{1}{2}$(y-x)=$\frac{1}{2}$(∠ACB-∠B).
(2)∠PED=$\frac{1}{2}$(∠C-∠B)
②∠E=$\frac{1}{2}$(∠ACB-∠B).证明如下:
设∠B=x,∠ACB=y,
因为AD平分∠BAC,
所以∠BAD=∠CAD=$\frac{1}{2}$∠BAC.
因为∠B+∠ACB+∠BAC=180°,
所以∠BAC=180°-x-y.
所以∠BAD=$\frac{1}{2}$(180°-x-y).
所以∠PDE=∠B+∠BAD=x+$\frac{1}{2}$(180°-x-y)=90°+$\frac{1}{2}$(x-y).
因为PE⊥AD,所以∠PDE+∠E=90°.
所以∠E=90°-[90°+$\frac{1}{2}$(x-y)]=$\frac{1}{2}$(y-x)=$\frac{1}{2}$(∠ACB-∠B).
(2)∠PED=$\frac{1}{2}$(∠C-∠B)
查看更多完整答案,请扫码查看


