《2025年新课程课堂同步练习册八年级数学上册华师大版》

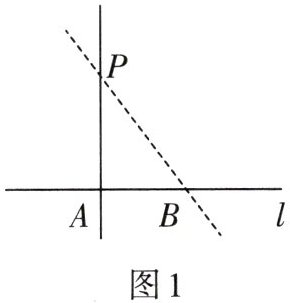
1. 用反证法证明“过直线外一点仅有一条直线与已知直线垂直”,有如下步骤：(如图1)
(1)故$\angle PAB+\angle PBA+\angle APB＞180^{\circ}$,这与三角形内角和定理相矛盾.
(2)$\therefore$假设不成立,原题成立.
(3)假设过$P$点不止一条直线与已知直线垂直,不妨设$PA\bot l于A$,$PB\bot l于B$.
(4)$\therefore\angle PAB = 90^{\circ}$,$\angle PBA = 90^{\circ}$.

正确的顺序应是(D)
A.(4)(3)(1)(2)
B.(1)(2)(3)(4)
C.(2)(3)(4)(1)
D.(3)(4)(1)(2)

答案： D

2. 用反证法证明“在$\triangle ABC$中,若$AB = AC$,则$\angle B＜90^{\circ}$”时,应假设(D)
A.$\angle B\neq 90^{\circ}$
B.$\angle B = 90^{\circ}$
C.$\angle B＞90^{\circ}$
D.$\angle B\geq 90^{\circ}$

答案： D

3. 用反证法证明命题时,首先要提出与结论相反(相排斥)的假设,若一个命题的结论是“$\angle A＞60^{\circ}$”,那么与它相反的假设应是(D)
A.$\angle A = 60^{\circ}$
B.$\angle A\neq 60^{\circ}$
C.$\angle A＜60^{\circ}$
D.$\angle A\leq 60^{\circ}$

答案： D

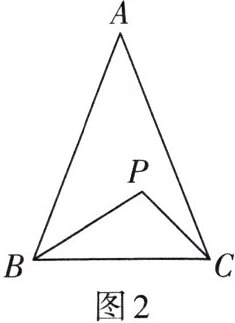
4. 如图2,在$\triangle ABC$中,$AB = AC$,$\angle APB\neq\angle APC$,求证：$PB\neq PC$.当用反证法证明时,第一步应假设(D)

A.$AB\neq AC$
B.$\angle B\neq\angle C$
C.$\angle APB= \angle APC$
D.$PB = PC$

答案： D

5. 用反证法证明“四边形中至少有一个角是钝角或直角”时,第一步应先假设命题不成立,则下列各备选项中,第一步假设正确的是(A)
A.假设四边形中没有一个角是钝角或直角
B.假设四边形中有一个角是钝角或直角
C.假设四边形中每一个角均为钝角
D.假设四边形中每一个角均为直角

答案： A

1. 用反证法证明“同位角不相等,两直线不平行”,应先提出假设两直线平行.

答案： 两直线平行

2. 用反证法证明命题“若$a$,$b$是整数,且$ab能被5$整除,那么$a$,$b中至少有一个能被5$整除”时,应假设a,b都不能被5整除.

答案： a,b都不能被5整除

3. 用反证法证明命题“三角形的三个外角中,最多有一个锐角”的第一步是假设三角形的三个外角中,至少有两个锐角.

答案： 三角形的三个外角中,至少有两个锐角