第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 在$\triangle ABC$中,$\angle A = 90^{\circ}$,下列式子中不成立的是(
A.$BC^{2} = AB^{2} + AC^{2}$
B.$AB^{2} = AC^{2} + BC^{2}$
C.$AB^{2} = BC^{2} - AC^{2}$
D.$AC^{2} = BC^{2} - AB^{2}$
B
)A.$BC^{2} = AB^{2} + AC^{2}$
B.$AB^{2} = AC^{2} + BC^{2}$
C.$AB^{2} = BC^{2} - AC^{2}$
D.$AC^{2} = BC^{2} - AB^{2}$
答案:
B
2. 直角三角形的两边长分别是$3和4$,则第三边长是(
A.$7$
B.$5$
C.$\sqrt{7}$
D.$\sqrt{7}或5$
D
)A.$7$
B.$5$
C.$\sqrt{7}$
D.$\sqrt{7}或5$
答案:
D
3. 如图1,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = 3$,$BC = 4$。以点$A$为圆心,$AC$长为半径画弧,交$AB于点D$,则$BD = $(
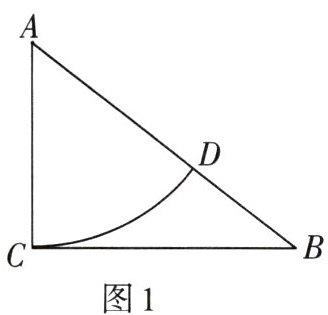
A.$2$
B.$3$
C.$4$
D.$5$
A
)
A.$2$
B.$3$
C.$4$
D.$5$
答案:
A
4. 意大利著名画家达芬奇用图2、图3所示的方法证明了勾股定理,图3是将图2沿直线$FD$剪开,将右半部分上下翻转得到的图形,其中四边形$AFEG$,四边形$CDBG与四边形A'E'B'C'$均为正方形,若图2中空白部分面积为$37$,线段$AB的长为7$,则图3中两个直角三角形的面积和为(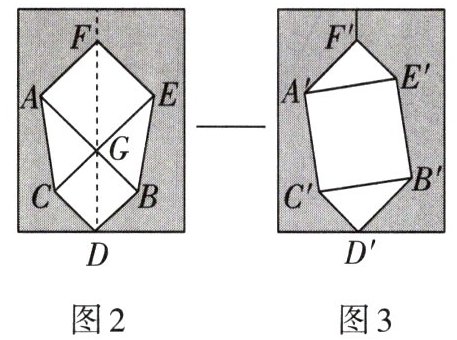
A.$6$
B.$12$
C.$15$
D.$25$
B
)
A.$6$
B.$12$
C.$15$
D.$25$
答案:
B
1. 在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$a$,$b$,$c分别是\angle A$,$\angle B$,$\angle C$所对的边。
(1)若$a = 5$,$b = 12$,则$c = $
(2)若$a = 16$,$c = 20$,则$b = $
(3)若$a:b = 3:4$,$c = 40$,则$a = $
(1)若$a = 5$,$b = 12$,则$c = $
13
;(2)若$a = 16$,$c = 20$,则$b = $
12
;(3)若$a:b = 3:4$,$c = 40$,则$a = $
24
。
答案:
(1)13
(2)12
(3)24
(1)13
(2)12
(3)24
2. 如图4,某住宅小区有一块长方形草地,一些人为了避开拐角走“捷径”,在草地内踩出了一条“路”。请算算他们仅仅少走了
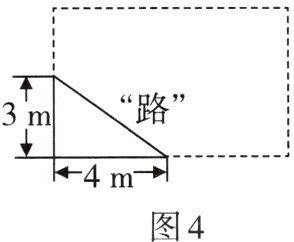
2
米路,却踩坏了草地。
答案:
2
3. 已知在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$BC = 6$,$AB - AC = 2$,则$AC = $
8
。
答案:
8
查看更多完整答案,请扫码查看


