第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
2. 如图9,C为BE上一点,点A,D分别在BE两侧. AB//ED,AB= CE,BC= ED. 求证:AC= CD.


答案:
证明:
∵AB//ED
∴∠B=∠E 又
∵AB=CE,BC=ED
∴△ABC≌△CED
∴AC=CD
∵AB//ED
∴∠B=∠E 又
∵AB=CE,BC=ED
∴△ABC≌△CED
∴AC=CD
3. 如图10,已知E是AB边的中点,AC与ED相交点F,且F是AC,DE的中点.
求证:(1)BE= CD;(2)BE//CD.
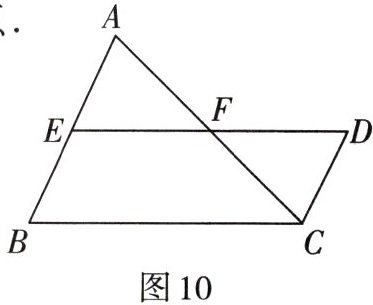
求证:(1)BE= CD;(2)BE//CD.

答案:
提示:
(1)利用SAS证明△AEF≌△CDF
(2)由△AEF≌△CDF得∠A=∠ACD即可
(1)利用SAS证明△AEF≌△CDF
(2)由△AEF≌△CDF得∠A=∠ACD即可
1. 在$\triangle ABC和\triangle DEF$中,$\angle A = \angle D$,$\angle B = \angle E$,要使$\triangle ABC\cong\triangle DEF$,需添加的条件是(
A.$AB = EF$
B.$AC = DE$
C.$BC = DF$
D.$AB = DE$
D
)A.$AB = EF$
B.$AC = DE$
C.$BC = DF$
D.$AB = DE$
答案:
D
2. 如图1,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$BC = 2\ cm$,$CD\perp AB$,在$AC上取一点E$,使$EC = BC$,过点$E作EF\perp AC交CD的延长线于点F$,若$EF = 5\ cm$,则$AE = $(

A.$5\ cm$
B.$3\ cm$
C.$2\ cm$
D.$1\ cm$
B
)
A.$5\ cm$
B.$3\ cm$
C.$2\ cm$
D.$1\ cm$
答案:
B
3. 如图2,在河对岸的$A$处有一座亭子,小宇站在点$B$处,为了求出自己与亭子的距离($AB$),小宇开展了实践活动,以下是打乱的活动流程:①在点$B同侧选择了一点C$,测得$\angle ABC = 65^{\circ}$,$\angle ACB = 30^{\circ}$;②用皮尺测得$BD = 26\ m$;③在$D$处立了一根标杆,使得$\angle CBD = 65^{\circ}$,$\angle DCB = 30^{\circ}$;④根据$\triangle ABC\cong\triangle DBC$,求出他与亭子之间的距离$AB = 26\ m$.正确的活动流程是(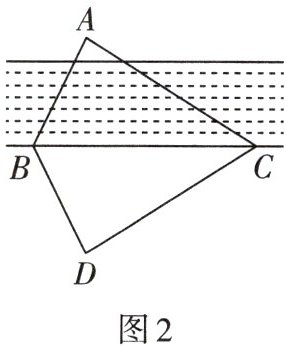
A.①②③④
B.②①③④
C.②③①④
D.①③②④
D
)
A.①②③④
B.②①③④
C.②③①④
D.①③②④
答案:
D
查看更多完整答案,请扫码查看


