第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
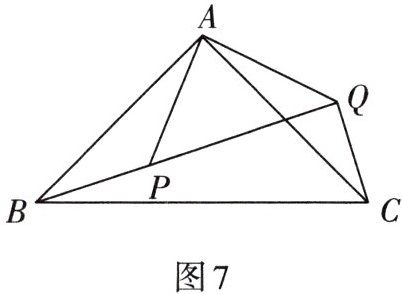
1. 如图7,在$△ABC$中,$AB= AC,∠BAC= 90^{\circ }$,P是$△ABC$内一点,将$△ABP$绕点A逆时针旋转一定角度后使得点B与点C重合.
(1)图中是否存在全等三角形?若存在,请写出两个全等的三角形,并写出它们的对应边及对应角;
(2)求$∠PAQ$的度数.
(1)图中是否存在全等三角形?若存在,请写出两个全等的三角形,并写出它们的对应边及对应角;
(2)求$∠PAQ$的度数.

答案:
(1)存在 △ABP≌△ACQ,对应边:AP和AQ,AB和AC,BP和CQ,对应角:∠ABP和∠ACQ,∠BAP和∠CAQ,∠APB和∠AQC
(2)90°
(1)存在 △ABP≌△ACQ,对应边:AP和AQ,AB和AC,BP和CQ,对应角:∠ABP和∠ACQ,∠BAP和∠CAQ,∠APB和∠AQC
(2)90°
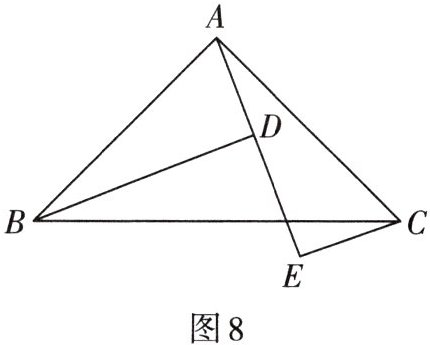
2. 如图8,A,D,E三点在同一条直线上,且$△BAD\cong △ACE$.
(1)求证:$BD= CE+DE$;
(2)当$∠BAC$满足什么条件时,$BD// CE$?并说明理由.
(1)求证:$BD= CE+DE$;
(2)当$∠BAC$满足什么条件时,$BD// CE$?并说明理由.

答案:
1. (1)
解:
因为$\triangle BAD\cong\triangle ACE$,根据全等三角形的性质,全等三角形的对应边相等,所以$BD = AE$,$AD = CE$。
又因为$AE=AD + DE$(线段的和差关系)。
把$BD = AE$,$AD = CE$代入$AE=AD + DE$中,可得$BD=CE + DE$。
2. (2)
解:
当$\angle BAC = 90^{\circ}$时,$BD// CE$。
理由:
因为$\triangle BAD\cong\triangle ACE$,所以$\angle ABD=\angle CAE$。
若$\angle BAC = 90^{\circ}$,则$\angle ABD+\angle BAD=\angle CAE+\angle BAD = 90^{\circ}$,所以$\angle ADB = 90^{\circ}$(三角形内角和为$180^{\circ}$,$\angle ADB=180^{\circ}-(\angle ABD + \angle BAD)$)。
又因为$\triangle BAD\cong\triangle ACE$,所以$\angle AEC=\angle ADB = 90^{\circ}$。
那么$\angle BDE = 180^{\circ}-\angle ADB=90^{\circ}$,所以$\angle BDE=\angle AEC$。
根据内错角相等,两直线平行,所以$BD// CE$。
综上,(1)得证$BD = CE + DE$;(2)当$\angle BAC = 90^{\circ}$时,$BD// CE$。
解:
因为$\triangle BAD\cong\triangle ACE$,根据全等三角形的性质,全等三角形的对应边相等,所以$BD = AE$,$AD = CE$。
又因为$AE=AD + DE$(线段的和差关系)。
把$BD = AE$,$AD = CE$代入$AE=AD + DE$中,可得$BD=CE + DE$。
2. (2)
解:
当$\angle BAC = 90^{\circ}$时,$BD// CE$。
理由:
因为$\triangle BAD\cong\triangle ACE$,所以$\angle ABD=\angle CAE$。
若$\angle BAC = 90^{\circ}$,则$\angle ABD+\angle BAD=\angle CAE+\angle BAD = 90^{\circ}$,所以$\angle ADB = 90^{\circ}$(三角形内角和为$180^{\circ}$,$\angle ADB=180^{\circ}-(\angle ABD + \angle BAD)$)。
又因为$\triangle BAD\cong\triangle ACE$,所以$\angle AEC=\angle ADB = 90^{\circ}$。
那么$\angle BDE = 180^{\circ}-\angle ADB=90^{\circ}$,所以$\angle BDE=\angle AEC$。
根据内错角相等,两直线平行,所以$BD// CE$。
综上,(1)得证$BD = CE + DE$;(2)当$\angle BAC = 90^{\circ}$时,$BD// CE$。
1. 如图1,下列条件能判定△ABO≌△DCO的是(
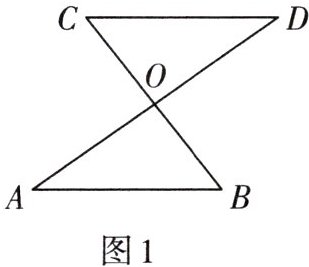
A.AB= CD,AO= CO
B.AB= CD,BO= CO
C.AO= DO,AB= CD
D.AO= DO,BO= CO
D
)
A.AB= CD,AO= CO
B.AB= CD,BO= CO
C.AO= DO,AB= CD
D.AO= DO,BO= CO
答案:
D
查看更多完整答案,请扫码查看


