《2025年绩优学案八年级数学上册人教版》

1. 如图1,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的(A)

A.三条中线的交点
B.三条角平分线的交点
C.三条高的交点
D.三边垂直平分线的交点

答案： A

2. 如图2,有一个厚薄均匀的三角形硬纸板,在硬纸板上选一点钻一个小孔,通过小孔系一条线将三角形硬纸板吊起,若三角形硬纸板处于平衡状态,则这一点可能是(A)

A.$N$点
B.$M$点
C.$P$点
D.$Q$点

答案： A

3. 平行四边形的重心是它的两条对角线的交点。

答案： 两条对角线的交点

4. 下列四个命题：①线段的重心就是线段的中点；②圆的重心就是圆心；③三角形的重心就是三角形三条高的交点；④四边形的重心就是两条对角线的交点。其中真命题是①②。(填序号)

答案： ①②

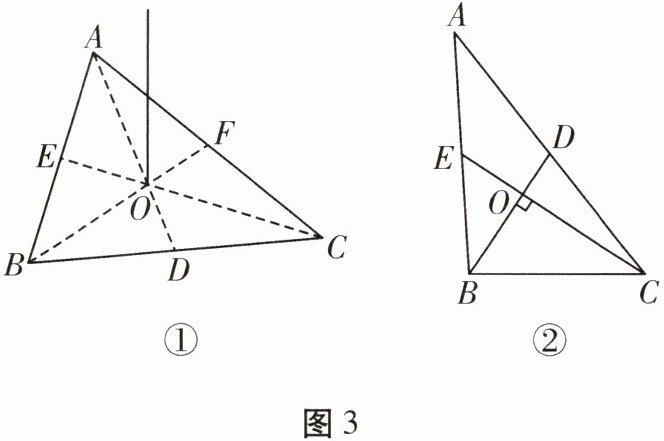
5. 取一块质地均匀的三角形纸板$ABC$,如果用一条细线从重心$O$处将三角形提起来,那么纸板就会处于水平状态。探究图①中$\frac{AO}{DO}$的值是多少。
吴老师为了让同学们更好地解决提出的问题,设置了以下两个任务,请同学们通过完成以下任务解决提出的问题。
【解决问题】任务1：若$\triangle BOC的面积为m$,求$\triangle AOB$的面积；
任务2：在任务1的条件下,求$\frac{AO}{DO}$的值。
【拓展应用】如图②,在$\triangle ABC$中,点$O是\triangle ABC$的重心。连接$BO$,$CO$并延长,分别交$AC$,$AB于点D$,$E$。若$BO\perp CO$,$BD = 6$,$CE = 9$,直接利用上面的结论,求四边形$AEOD$的面积。

活动二 确定平面组合图形的重心位置
【解题技巧】在平面内,图形$A与图形B拼成图形C$,图形$A的重心坐标为(x_1,y_1)$,面积为$S_1$,图形$B的重心坐标为(x_2,y_2)$,面积为$S_2$,则图形$C的重心坐标为(\frac{S_1x_1 + S_2x_2}{S_1 + S_2},\frac{S_1y_1 + S_2y_2}{S_1 + S_2})$,且图形$C的重心一定在图形A的重心与图形B$的重心连接的线段上。

答案： 解:【解决问题】任务1:
∵ 点O为△ABC的重心，
∴ D,E,F分别是BC,AB,AC边的中点，
∴ $ S_{\triangle ABF}=S_{\triangle CBF} $, $ S_{\triangle OAF}=S_{\triangle OCF} $，
∴ $ S_{\triangle AOB}+S_{\triangle OAF}=S_{\triangle BOC}+S_{\triangle OCF} $，
∴ $ S_{\triangle AOB}=S_{\triangle BOC}=m $。
任务2:由题意可知 $ S_{\triangle OCD}=S_{\triangle OBD}=\frac{1}{2}S_{\triangle BOC}=\frac{1}{2}m $, $ S_{\triangle OBE}=S_{\triangle OAE} $，
$ S_{\triangle AOB}=S_{\triangle BOC}=m $,
∴ $ \frac{S_{\triangle AOB}}{S_{\triangle OBD}}=\frac{m}{\frac{1}{2}m}=2 $。
∵ △AOB与△OBD同高，
∴ $ \frac{S_{\triangle AOB}}{S_{\triangle OBD}}=\frac{AO}{DO}=2 $,即$ \frac{AO}{DO}=2 $。
【拓展应用】
∵ 点O是△ABC的重心,类比任务1、任务2可知 $ S_{\triangle BCE}=S_{\triangle ACE} $,$ \frac{OB}{OD}=\frac{OC}{OE}=2 $,
∵ BD=6,CE=9,
∴ OD=2,OB=4,OE=3,OC=6。
∵ BO⊥CO,
∴ $ S_{\triangle ACE}=S_{\triangle BCE}=\frac{1}{2}CE\cdot OB=\frac{1}{2}× 9× 4=18 $,
$ S_{\triangle COD}=\frac{1}{2}OC\cdot OD=\frac{1}{2}× 6× 2=6 $,
∴ $ S_{四边形AEOD}=S_{\triangle ACE}-S_{\triangle COD}=18-6=12 $。