《2025年新课程课堂同步练习册七年级数学上册人教版》

3. 某同学在计算一个多项式减去$2ab - 3bc - ac$时,误认为是加上此式,该同学计算出的结果为$ab - 3bc + 4ac$。试求出正确运算的结果。

答案： 依题意有：$(ab-3bc+4ac)-(2ab-3bc-ac)=ab-3bc+4ac-2ab+3bc+ac=-ab+5ac$，$(-ab+5ac)-(2ab-3bc-ac)=-ab+5ac-2ab+3bc+ac=-3ab+6ac+3bc$

4. 数学活动：将连续的奇数$1$,$3$,$5$,$7$,…$$排成如下的数表,用十字框框出$5$个数,请回答：
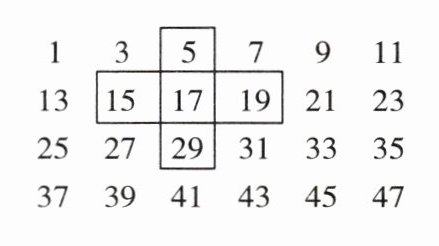
(1)框出的$5个数的和与框中最中间的数17$有什么关系？
(2)在数表中,用十字框任意框出$5$个数,并设最中间的数为$a$,用整式表示十字框框出的$5$个数之和是多少？
(3)十字框框出的$5个数之和能等于2010$吗？若能,请写出这$5$个数；若不能,请说明理由。

答案：
(1)框出5个数之和为85，是17的5倍
(2)$5a$
(3)因为$5a=2010,a=402$，表中全是奇数，不可能是402，所以5个数之和不可能等于2010