《2025年新课程课堂同步练习册七年级数学上册人教版》

1. 如图2,观察下列图形的构成规律,按此规律,第$6$个图形中棋子的个数为19个,第$n$个图形中棋子的个数为$(3n+1)$个.

答案： 19,$(3n+1)$

2. 已知：$a_{4}x^{4} + a_{3}x^{3} + a_{2}x^{2} + a_{1}x + a_{0} = 6x$,则
(1)取$x = 0$时,可以得到$a_{0} = $0；
(2)取$x = 1$时,可以得到$a_{4} + a_{3} + a_{2} + a_{1} + a_{0} = $6；
(3)取$x = -1$时,可以得到$a_{4} - a_{3} + a_{2} - a_{1} + a_{0} = $-6.

答案： 0,6,-6

3. 当$x = 1$时,代数式$ax^{5} + bx^{3} + cx - 7的值为10$,则当$x = -1$时,求代数式$ax^{5} + bx^{3} + cx - 7$的值是-24.

答案： -24

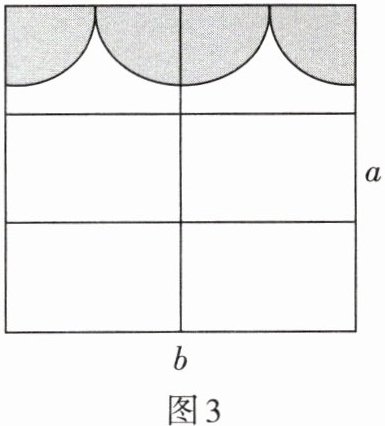
4. 小明房间的窗户如图3所示,其中上方的装饰物由两个四分之一圆和一个半圆组成,他们的半径相同,用含有$a$,$b$的代数式表示窗户中透光部分的面积是$ab-\dfrac{\pi}{16}b^{2}$(窗框面积忽略不计,结果保留$\pi$).

答案： $ab-\dfrac{\pi}{16}b^{2}$

1. 图4是一个圆环,外圆和内圆的半径分别是$R和r$,(1)用代数式表示圆环面积；(2)当$R = 5\ cm$,$r = 2\ cm$时,圆环的面积是多少($\pi取3.14$)？

答案：
(1)圆环面积=$\pi(R^{2}-r^{2})\ cm^{2}$
(2)当$R=5\ cm,r=2\ cm$时,圆环面积=$\pi(5^{2}-2^{2})\approx65.94\ cm^{2}$